密码学知识（二）

1.PRG的安全性定义

  由于无法达到真正的随机，只能通过人为的算法无限逼近随机，所以伪随机算法诞生。只要无限逼近这个极限，就认为是一个随机产生的序列。

  用通俗的话解释，PRG模型其实就是一个将短的比特串变成长比特串的过程，这个变换的过程我们并不关心。

 

2.PRG的安全模型

  首先设 G: {0,1}s → {0,1}n 是一个PRG。下面给出PRG的安全模型：

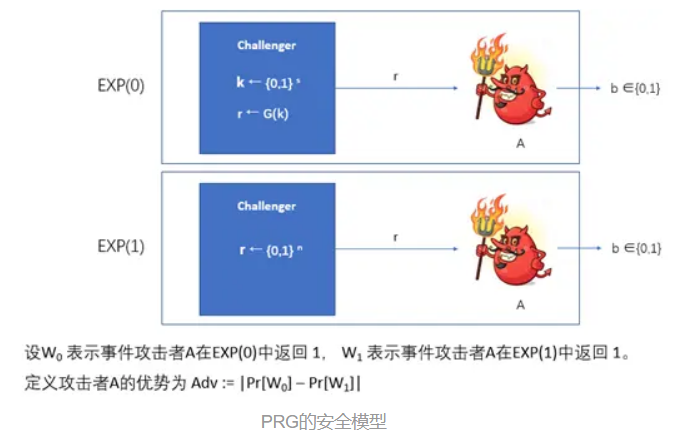
  设A是一个攻击者，用一个红色小怪物来表示。构造两个“小黑屋”，也即黑盒子（black box），每个屋里各有一个挑战者（challenger）：

1. 一个挑战者执行G，随机选择种子k，并将G（k）的执行结果返回给A。

2. 另一个 挑战者随机选择r，并将之直接返回给A。

3. 随机选择一个小黑屋，放到A的面前，A并不知道自己面对的是哪一个小黑屋：

   如果A面对的是PRG的小黑屋，我们称实验为EXP(0)。

   如果A面对的是随机序列的小黑屋，我们称为EXP(1)。

4. A根据r猜测自己面对的是哪个小黑屋，并输出自己的猜测b。

 

3.EAV-Security（多消息窃听实验）

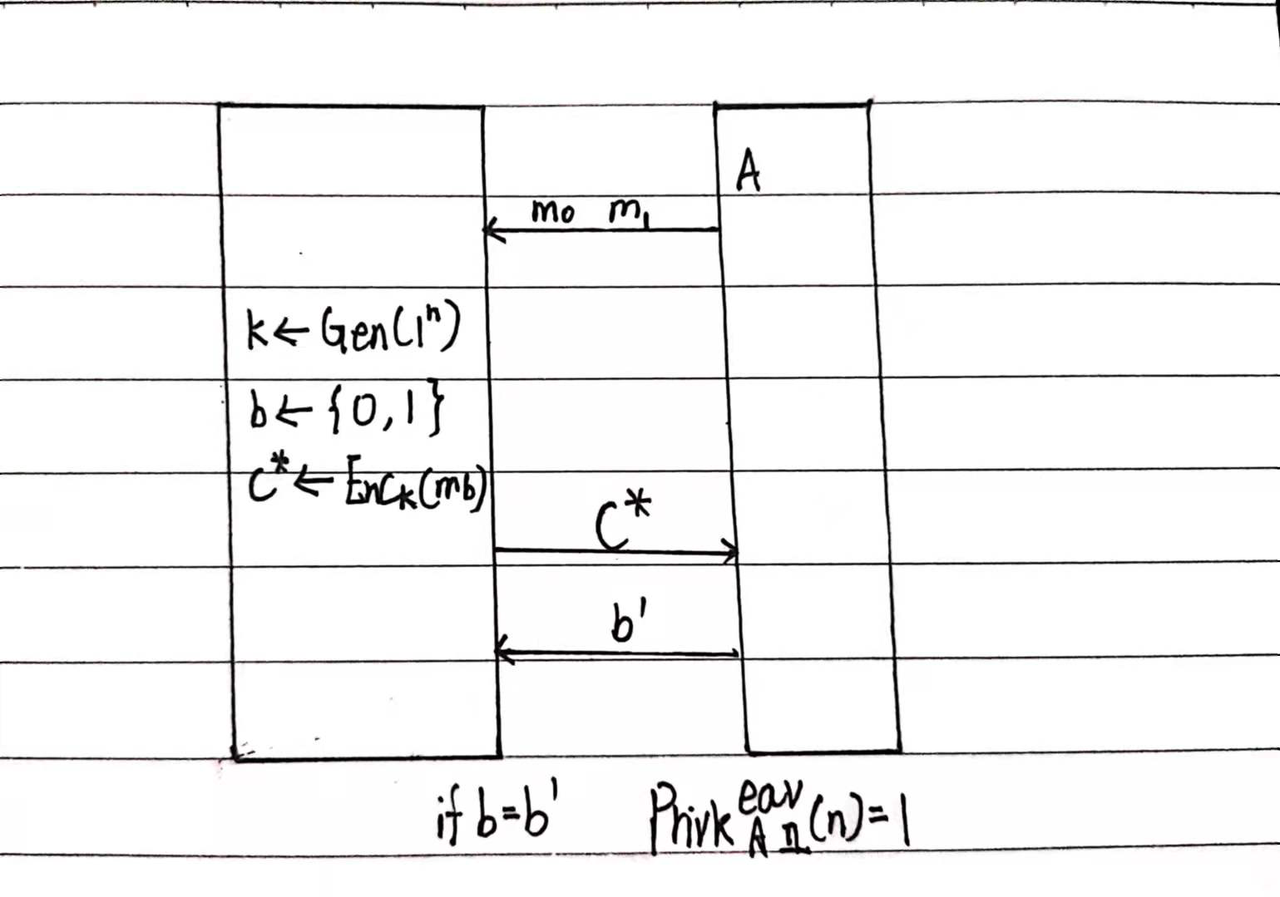
  Privk（交互机模型）

  EAV的单消息安全并不代表多消息安全

 

4.证明题一：if G is PRG,then Π is eav—secure

  PPT:概率时间多项式时间算法

 

5.加密方案的攻击类型

1. 唯密文攻击：攻击者只知道一些密文
2. 已知明文攻击：攻击者除了知道一些密文以外，还可以通过某些手段知道这些密文对应的明文。
3. 选择明文攻击（CPA）：攻击者自己选择一些明文，并可以通过某些手段获得相应的密文。
4. 选择密文攻击（CAA）：攻击者自己选择一些密文，并可以通过某些手段获得相应的明文。

 

6.语义安全性

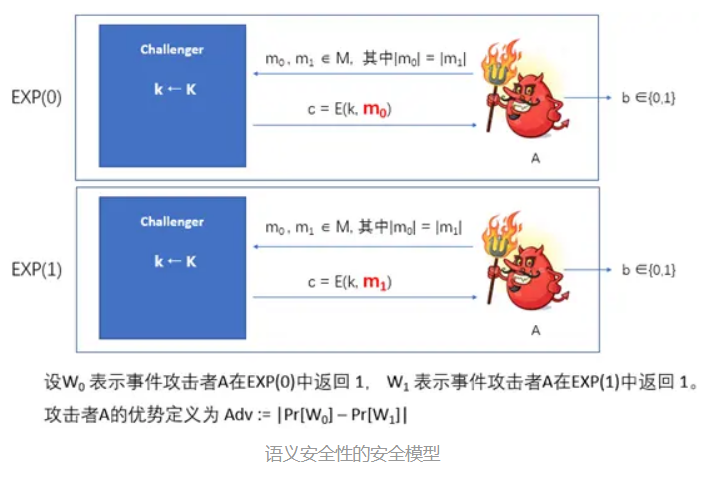
1. 挑战者会从密钥空间K中随机选择一个密钥k，并对攻击者A发送的两个明文中的其中一个就行加密，在实验EXP(0)中，挑战者加密的是明文m0，而在实验EXP(1)中加密的是m1。
2. A根据获得的密文c猜测自己是处于哪个实验中，并输出自己的猜测，记为b。
3. A只能给挑战者发送一次明文，也即只允许A询问一次，换句话说，挑战者选择的密钥只使用一次。

  以此安全模型为基础，定义语义安全：

  利用定义得出语义安全性的公式表达：

  本质：如果加密算法是语义安全的，则m0和m1的密文计算上是不可区分的。

 

7.分组密码的定义

  PRF：Pseudorandom Functions 伪随机函数:

  随机函数（即是定义在一堆规则的函数中随机挑选一个函数）：

 

8.PRF的安全模型

  根据随机函数的概念，定义PRF的安全性：

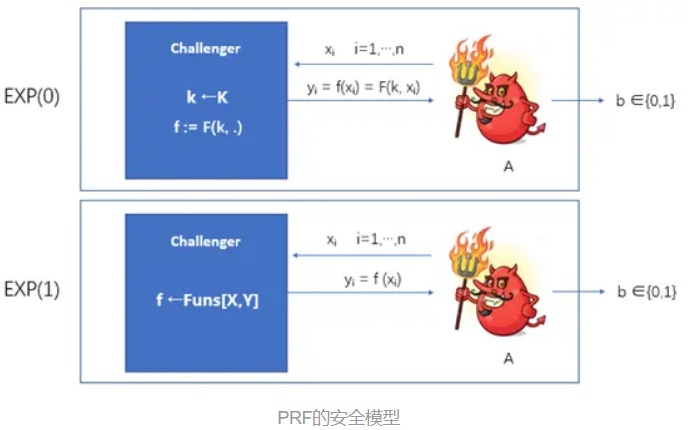
  在PRF的安全模型中，同样考虑两个挑战者，每个挑战者都控制着一个函数f

  第一个挑战者的函数为f := F (k, .)；i（真随机对应函数）。

  第二个挑战者则是从随机函数Funs[X,Y]中随机选择一个函数。

  攻击者 A 不知道自己面对的挑战者到底是哪一个，但他可以通过“探测”的方法来帮助判断。A 的最终目标就是要猜出自己面对的到底是哪一个挑战者。

  探测的方法是这样的：A 可以向挑战者发送一个元素 x_i∈X，挑战者将相应的 y_i:= f(x_i) 返回给 A。

  A 可以进行这样的探测很多次。

  当然，A 可以根据前一次探测得到的y_i来产生下一次探测时使用的x_{i+1}，以根据它们之间的关系来判断到底挑战者是哪一个，也即面前的挑战者控制的函数到底是哪一种类型：使用随机密钥的 PRF，还是随机函数。

  定义 (安全的 PRF)：如果所有高效的攻击者的优势都是可忽略的，那么该 PRF 是安全的。

 

9.PRP的安全定义

  一个分组密码其实也可以被称之为伪随机置换（PRP），因为分组密码和PRF的定义及安全模型是非常类似的，分组密码的安全性要求其与随机置换在计算上不可区分。

  通过定义可以知道，PRF 和 PRP（分组密码）之间最主要的区别就是，PRP 是有逆函数的，而 PRF 未必有逆函数。

  （本质就是X和Y都是相同的区域空间，相互映射）