线性表

1.知识框架

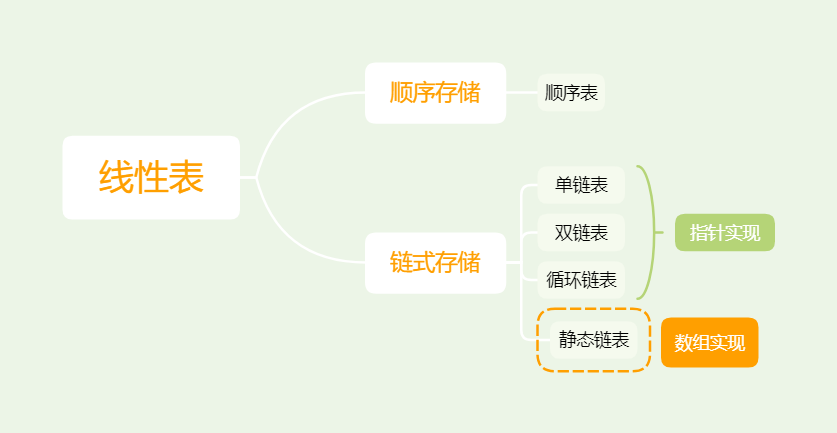
2.线性表的基本术语

线性表是具有相同数据类型的n（n≥0）个数据元素的有限序列：

在线性表中ai是线性表中第i个元素的位序（位序冲1开始，数组下标从0开始），并且除第一个元素外，每个元素有且仅有一个直接前驱；除最后一个元素外，每个元素有且仅有一个直接后继

3.线性表的基本操作

InitList(&L)    //初始化表，构建一个空的线性表
Length(L)  //求表长，返回表的长度，即表L中数据元素的个数
    
LocateElem(L,e) //按值查找操作，在表中查找具有给定关键字值的元素
GetElem(L,i) //按位查找，获取表中第i个位置的元素的值
    
ListInsert(&L,i,e)  //插入操作，在表L中第i个位置上插入指定元素e
ListDelete(&L,i,&e)   //删除操作，删除表L第i个位置的元素，并用e返回删除元素的值
    
PrintList(L) //输出操作，按前后顺序输出线性表L的所有元素值
Empty(L)     //判空操作，若L为空表则返回ture，反之则返回false
DestroyList(&L)  //销毁操作，销毁线性表并释放相关的内存

4.顺序表的定义

顺序表是指线性表的顺序存储方式，它用一组地址连续的存储单元依次存储线性表中的数据元素，从而使得逻辑上相邻的两个元素在物理位置上也是相邻的。

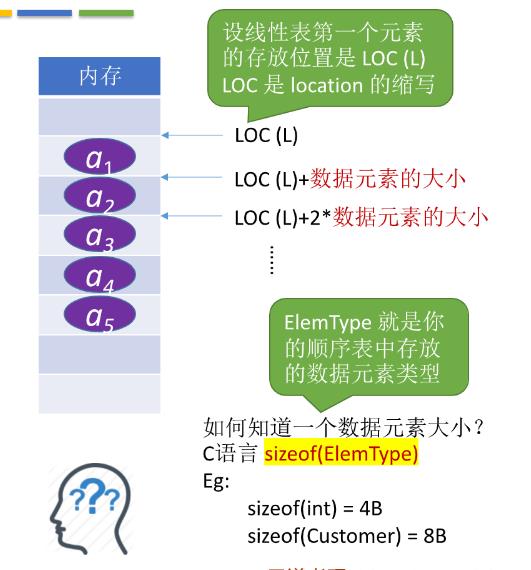
每一个数据元素的存储位置都和线性表的起始位置相差一个和该数据元素的位序成正比的常数，因此，线性表的任一数据元素都可以随机存取，所以线性表的顺序存储结构是一种随机存取的存储结构。

5.数组分配类别

一维数组可以是静态分配，也可以是动态分配的，在静态分配时，由于数组的大小和空间已经提前固定，一旦空间占满，再加入新的数据就会产生溢出，进而导致程序崩溃，而在动态分配时，储存数组的空间是在程序执行过程中通过动态存储分配语句分配的，一旦数据空间占满，就会另外开辟一块更大的存储空间，用以替换原来的存储空间，从而达到扩充存储数组的目的

静态分配

#include <stdio.h>
#define MaxSize 10  //定义最大长度

typedef struct{
    int data[MaxSize];   //用静态的“数组”存放数据元素
    int length;          //顺序表的当前长度
}SqList;                 //顺序表的类型定义

//初始化顺序表
void InitList(SqList &L){
    for(int i=0;i<MaxSize;i++)
    {
        L.data[i]=0;             //数据元素初始值默认为0
    }
    L.length=0;                 //顺序表初始化长度为0
}

int main(){
    SqList L;               //声明一个顺序表
    InitList(L);            //初始化顺序表
    return 0;
}

动态分配

#include <stdio.h>
#include <stdlib.h>
#define InitSize 10  //定义顺序表的初始长度

typedef struct{
    int *data;   //动态分配数组的指针
    int MaxSize        //顺序表的最大容量
    int length;          //顺序表的当前长度
}SeqList;                 //顺序表的类型定义

void InitList(SeqList &L){
    //使用malloc函数申请一片连续的空间
    L.data = (int *)malloc(InitSize*sizeof(int));
    L.length = 0;
    L.MaxSize = InitSize
}

//增加动态数组的长度
void IncreaseSize(SeqList &L,int len){
    int *p = L.data;
    L.data = (int *)malloc((L.MaxSize+len)*sizeof(int));
    for(int i=0;i<L.length;i++){
        L.data[i]=p[i];            //迁移数据
    }
    L.MaxSize = L.MaxSize+len;     //数据最大长度增长len
    free(p);                      //释放原来的内存空间
}

int main(){
    SeqList L;
    InitList(L);
    IncreaseSize(L,5);
    return 0;
}

6.三种基本操作的实现

插入操作

#include <stdio.h>
#define MaxSize 10  //定义最大长度

typedef struct{
    int data[MaxSize];   //用静态的“数组”存放数据元素
    int length;          //顺序表的当前长度
}SqList;                 //顺序表的类型定义

//初始化顺序表
void InitList(SqList &L){
    for(int i=0;i<MaxSize;i++)
    {
        L.data[i]=0;             //数据元素初始值默认为0
    }
    L.length=0;                 //顺序表初始化长度为0
}

//插入顺序表
void ListInsert(SqList &L,int i,int e){
    for(int j=L.length;j>=i;j--)
    {
        L.data[j]=L.data[j-1];
    }
    L.data[i-1]=e;
    L.length++;
}

int main(){
    SqList L;               //声明一个顺序表
    InitList(L);            //初始化顺序表
    
    LISTiNSERT(L,3,3);     //插入元素
    return 0;
}

删除操作

#include <stdio.h>
#define MaxSize 10  //定义最大长度

typedef struct{
    int data[MaxSize];   //用静态的“数组”存放数据元素
    int length;          //顺序表的当前长度
}SqList;                 //顺序表的类型定义

//初始化顺序表
void InitList(SqList &L){
    for(int i=0;i<MaxSize;i++)
    {
        L.data[i]=0;             //数据元素初始值默认为0
    }
    L.length=0;                 //顺序表初始化长度为0
}

//删除顺序表
void ListDelete(SqList &L,int i,int e){
    e=L.data[i-1];
    for(int j=i;j>L.length;j++)
    {
        L.data[j-1]=L.data[j];
    }  
    L.length--;
}

int main(){
    SqList L;               //声明一个顺序表
    InitList(L);            //初始化顺序表
    
    ListDelete(L,3,e);     //删除元素
    return 0;
}

按位查找

1
2
3

int GetElem(SeqList L, int i){
    return L.data[i-1];
}

按值查找

int LocateElem(SeqList L,int e){
    for(int i=0;i<L.length;i++)
        if(L.data[i]==e)
        {
            return i+1;
        }
    return 0;
}

7.单链表的定义

线性表的链式存储又称单链表，它是指通过一组任意的存储单元来存储线性表中的数据元素。为了建立数据元素之间的线性关系，对每个链表结点，出存放元素自身的信息外，还需要存放一个指针

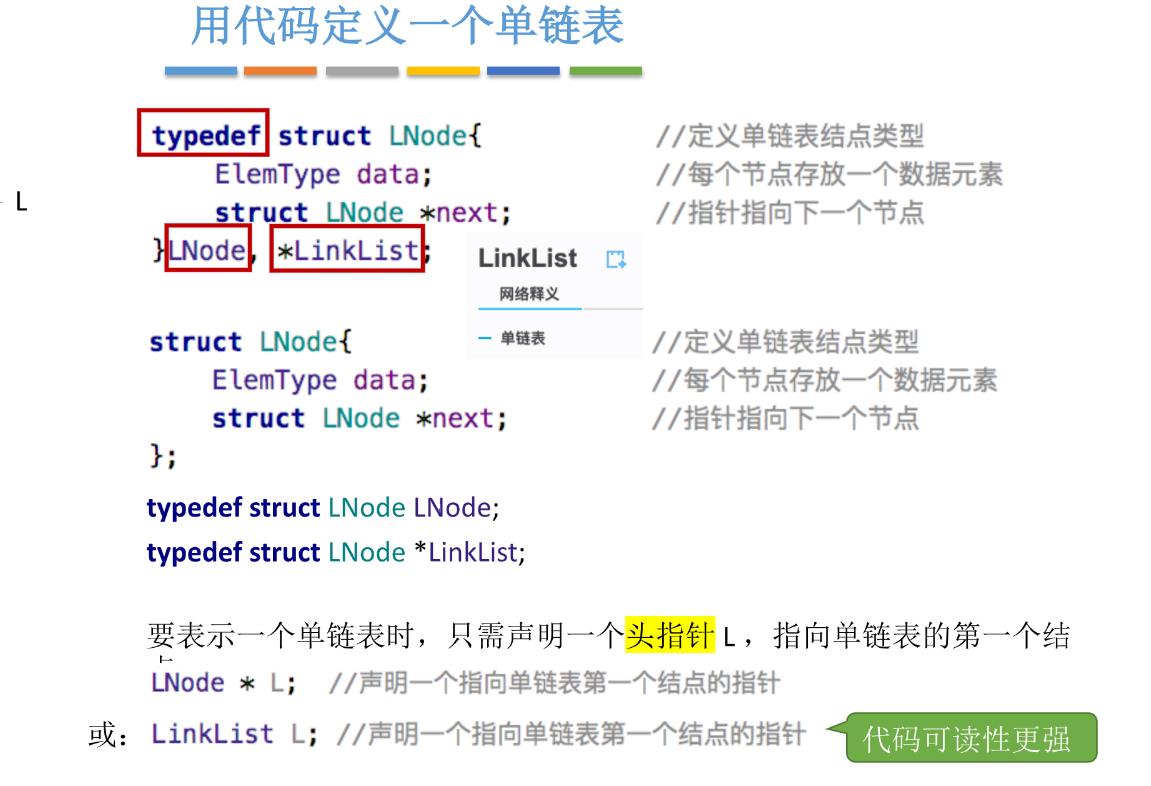
单链表作为非随机存取的存储结构，并不能直接找到表中某个特定的结点，查找某个特定的结点时，需要从表头开始遍历，依次查找。通常而言，单链表用头指针来标识一个单链表，比如单链表为L，头指针为NULL时表示一个空表，此外为了方便操作，在单链表第一个结点之前附加了一个结点，称为头结点。

typedef struct LNode{
    ElemType data;
    struct LNode *next;
}LNode,*LinkList;

8.单链表的建立

尾插法建立单链表

LinkList List_TailInsert(LinkList &L){
    int x;
    L=(LinkList)malloc(sizeof(LNode));
    LNode *s,*r=L;
    scanf("%d",&x);
    while(x!=9999){
        s=(LNode *)malloc(sizeof(LNode));
        s->data=x;
        s->next=s;
        r=s;
        scanf("d",&x);
    }
    r->next=NULL;
    return L；
}

头插法建立单链表

LinkList List_HeadInsert(LinkList &L){
    LNode *s
    int x;
    L=(LinkList)malloc(sizeof(LNode));
    L->next=NULL;
    LNode *s,*r=L;
    scanf("%d",&x);
    while(x!=9999){
        s=(LNode *)malloc(sizeof(LNode));
        s->data=x;
        s->next=L->next;
        L->next=s;
        scanf("d",&x);
    }
    return L；
}

9.按位序插入

带头结点

bool ListInsert(LinkList &L,int i,ElemType e){
    if(i<0)    //判断非法输入
    {
        return false
    }
    LNode *p;     //指针p指向当前扫描到的结点
    int j=0;     //j为p当前指向的结点位置
    p = L;       //L指向头检点，头结点作为第0个结点是不存在数据的
    while(p!=NULL && j<i-1)    //循环找到第i-1个结点
    {
        p=p->next;
        j++; 
    }
    if(p==NULL)
    {
        return false;
    }
    LNode *s=(LNode *)malloc(szieof(LNode));
    s->data = e;
    s->next=p->next;
    p->next=s;       //将结点s连到p之后
    return ture;    //插入成功
}

不带头结点

bool ListInsert(LinkList &L,int i,ElemType e){
    if(i<1)    //判断非法输入
    {
        return false
    }
    if(i=1)
    {
        LNode *s = (Lnode *)malloc(sizeof(LNode));
        s->data=e;
        s->next=L;
        L=s;
        return ture
    }
    LNode *p;     //指针p指向当前扫描到的结点
    int j=1;     //j为p当前指向的结点位置
    p = L;       //L指向头检点，头结点作为第0个结点是不存在数据的
    while(p!=NULL && j<i-1)    //循环找到第i-1个结点
    {
        p=p->next;
        j++; 
    }
    if(p==NULL)
    {
        return false;
    }
    LNode *s=(LNode *)malloc(szieof(LNode));
    s->data = e;
    s->next=p->next;
    p->next=s;       //将结点s连到p之后
    return ture;    //插入成功
}

10.指定结点插入

后插操作

bool InsertNext(LNode *p, ElemType e)
{
    if (p==NULL)
        return false
    LNode *s = (LNode *)malloc(sizeof(LNode)) ;
    if (s == NULL)
        RETURN FALSE;
    s->data = e;
    s->next = p->next;
    p->next = s;
    return ture;
}

前插操作

bool InserstPriorNode(LNdoe *p, LNode *s)
{
    if(p==NULL||S==NULL)
        return false;
    s->next = p->next;
    p->next = s;
    ElemType temp = p->data;
    p->data = s->data;
    s->data = temp;
    return ture;
}

11.指定结点删除

带头结点

bool DeleteNode(LinkList &p)
{
    if(p==NULL)
        return false;
    LNode *q=p->next
    p->data=p->next->data;
    p->next=q->next;
    free(q);
    return ture;
}

12.单链表查找

按位查找

LNode *GetElem(LinkList L,int i)
{
    if(i<0)
        return NULL;
    LNode *p;
    int j=0;
    p=L;
    while(p!=NULL && j<i<1)
    {
        p=p->next;
        j++;
    }
}

按值查找

LNode *LocateElem(LinkList L,ElemType e)
{
    LNode *p = L->next;
    while(p!=NULL && p->data!=e)
        p = p->next;
    return p;       //找到后返回该结点指针，否则返回NULL
}

13.双链表初始化

带头结点

typedef struct DNode
{
    ElemType data;
    struct DNode *prior,*next;
}DNode,*DLinklist;

bool InitDLinkList(DLinklist &L)
{
    L = (DNode *)malloc(szie(DNode));
    if(L==NULL)
        return false;
    L->prior = NULL;
    L->next = NULL;
    return ture;
}

14.双链表插入

bool InsertNextDNode(DNode *p,DNode *s)
{
    if(p==NULL ||s==NULL)
        return false;
    s->next=p->next;
    if(p->next!=NULL)  //如果p结点有后继结点
        p->next->prior=s;
    s->prior=p;
    p->next=s;
    return true;    
}

15.双链表删除

bool DeleteNDode(DNode *p)
{
    if (p==NULL)
        return false;
    DNode *q = p->next;  //找到p的后继节点q
    if(q==NULL)          //p没有后继结点情况
        return false;
    p->next=q->next;
    if(q->next!=NULL)    //
        q->next->prior=p;
    free(q);
    return true
}

16.循环链表

循环单链表

typedef struct LNode
{
    ElemType data;
    struct LNode *next;
}LNode,*LinkList;

bool InitList(LinkList &L)
{
    L = (LNode *)malloc(szieof(LNode));
    if(L=NULL)
        return false;
    L->next = L;     //头结点next指向头结点
    return true;
}

循环双链表

typedef struct DNode
{
    ElemType data;
    struct LNode *prior,*next;
}DNode,*DLinkList;

bool InitDLinkList(DLinkList &L)
{
    L = (DNode *)malloc(szieof(DNode));
    if(L=NULL)
        return false;
    L->prior = L;
    L->next = L;     //头结点next指向头结点
    return true;
}

17.静态链表（考察不多）

静态链表：分配一整片连续的内存空间，所有结点集中安置

创建静态链表

#define MaxSize 10
struct Ndoe
{
    ElemType data;
    int next;
};

适用于不支持指针的低级语言和数据元素数量固定不变的场景。

18.顺序表vs链表

逻辑结构：

都属于线性表，都是线性结构

存储结构

顺序表是顺序存储，优点是支持随机存取，存储密度高，但是存在大片连续看见分配不方便，改变容量不方便；链表是链式存储，优点是离散的小空间分配方便，改变容量方便，但是存在不可随机存取，存储密度低的问题

基本操作

创建、销毁（考察不多）、增、删、改、查

问题举例

数据结构学习笔记

线性表

https://one-null-pointer.github.io/2022/09/17/数据结构二/

Author

liaoyue

Posted on

September 17, 2022

传送口

前言 Previous

绪论 Next

线性表

线性表

1.知识框架

2.线性表的基本术语

3.线性表的基本操作

4.顺序表的定义

5.数组分配类别

6.三种基本操作的实现

插入操作

删除操作

按位查找

按值查找