栈

1.栈的定义

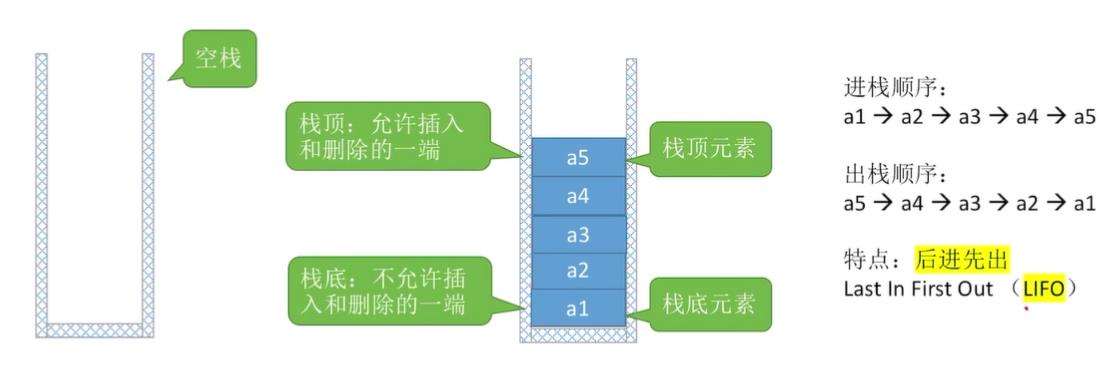
  简单的理解，栈是只允许在一端进行插入或者操作的线性表

 

2.栈的基本操作

• InitStack(&S)：初始化栈。构造一个空栈，分配内存空间。
• DestroyStack(&L)：销毁栈。销毁并释放栈S所占用的内存空间
• Push(&S,x)：进栈，若栈S未满，则将x加入栈中成为新的栈顶
• Pop(&S,&x)：出栈，若栈S非空，则弹出栈顶元素，并用x返回
• GetTop(S,&x)：读栈顶元素，用x返回栈顶元素

 

3.顺序栈

• 定义

#define MaxSize 10
typrdef struct
{
    ElemType data[MaxSize];    //静态数组存放栈中的元素
    int top;
}SqStack;

• 初始化

voif InitStack(SqStack &s)
{
    s.top=-1;
}

• 进栈

bool Push(SqStack &S,ElemType x)
{
     if(S.top==MaxSize-1)
         return false;
    S.top = S.top + 1;
    S.data[S.top]=x;
    return true;     
}

• 出栈

bool Pop(SqStack &S,ElemType &x)
{
     if(S.top==-1)
         return false;
    x=S.data[S.top];
    S.top = S.top-1;
    return true;     
}

• 共享栈

 

4.链栈

  使用链式存储方式实现的栈，实现头插和后删的单链表

typedef struct Linknode
{
    ElemType data;
    struct Linknode *next;
}*LiStack;

 

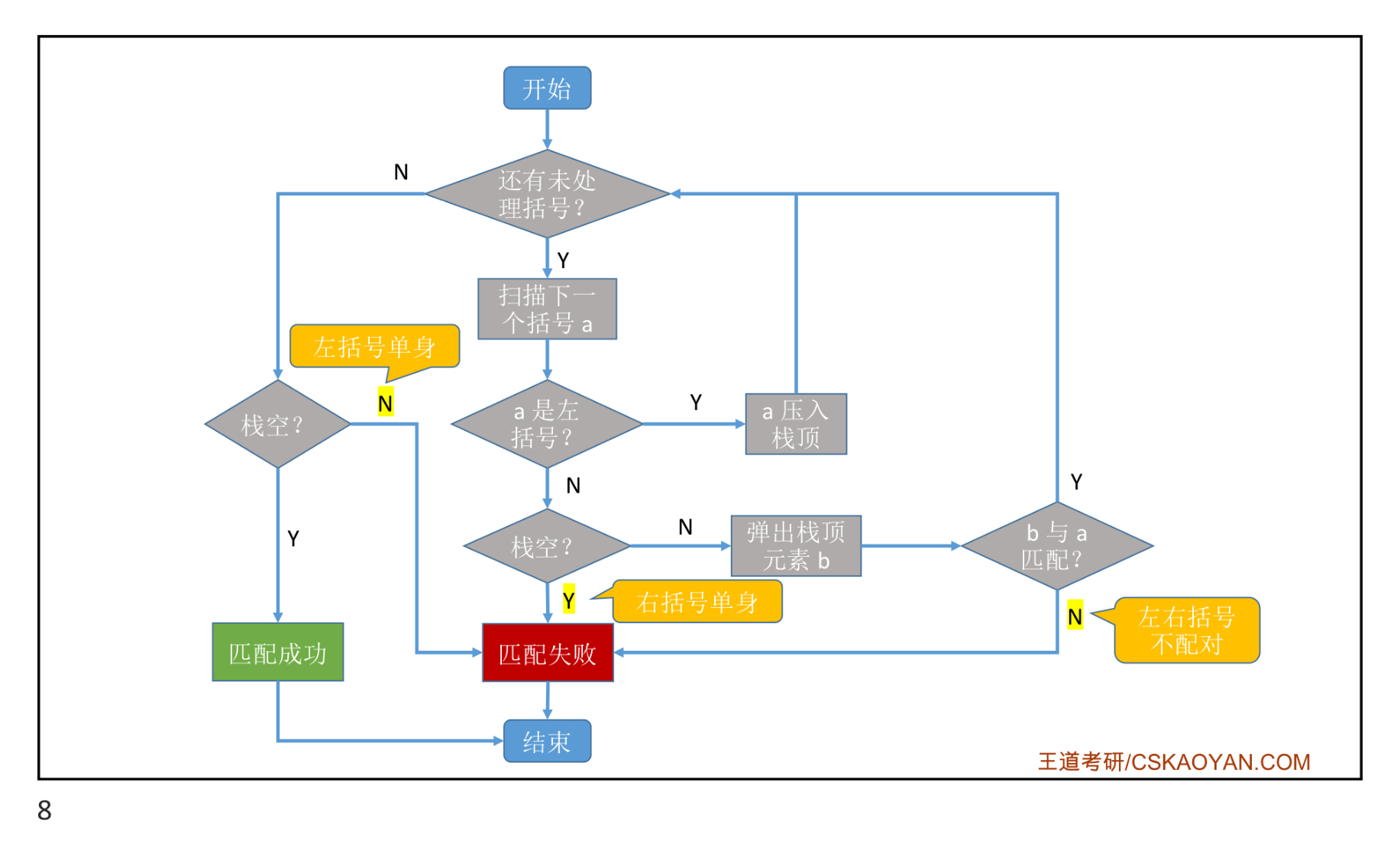
5.栈的应用——括号匹配

• 流程图

bool bracketCheck(char str[],int length)
{
    SqSTACK S;
    InitStack(S);
    for(int i=0;i<length;i++)
    {
        if(str[i]=='('||str[i]=='['||str[i]=='{')   //扫描左括号
        {
            Push(S,str[i]);
        }
        else
        {
            if(StackEmpty(S))
            {
                return false;
            }
            char topElem;
            Pop(S,topElem);     //栈顶元素出栈
            if(str[i]==')'&&topElem!='(')
                return false;
            if(str[i]==']'&&topElem!='[')
                return false;
            if(str[i]=='}'&&topElem!='{')
                return false;           
        }
    }
    return false;
}

• 总结

  用栈实现括号匹配，依次扫描所有字符，遇到左括号入栈，遇到有括号则弹出栈顶元素检查是否匹配，匹配失败的情况只有三种：左括号单一，右括号单一，左右括号不匹配。

 

6.栈的应用——表达式求值的应用

•   三种形式的表达式（后缀表达式为重点内容）

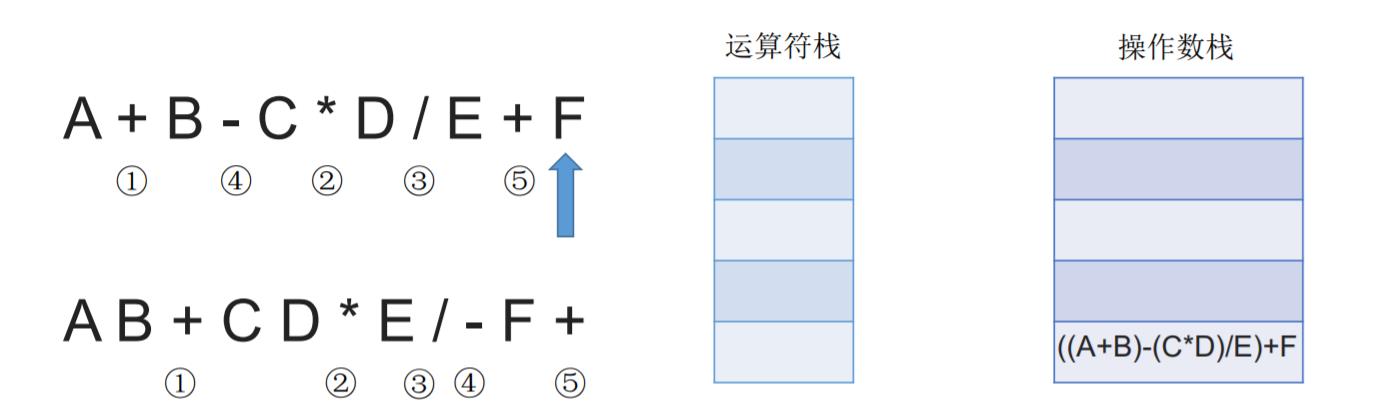
  后缀表达式采用”左优先原则”：只要左边的运算符能先计算，就优先计算左边的。

  前缀表达式采用“右优先原则”：只要右边的运算符能先计算，就优先计算右边的。

• 中缀表达式转后缀表达式并计算的实现原理

  用栈实现中中缀表达式的计算：首先初始化两个栈，操作数栈和运算符栈，若扫描到操作数，压入操作数栈，若扫描到运算符或界限符，则按照“中缀转后缀 ”相同的逻辑压入运算符栈（期间也会弹出运算符，每当弹出一个运算符时，就需要再弹出两个操作数栈的栈顶元素并执行相应运算，运算结果再压回操作数栈中）

 

8.栈的应用——递归的应用

• 函数调用特点

  函数调用的特点是最后被调用的函数最先执行结束，函数调用时，需要用一个栈存储，包括调用返回地址、实参、局部变量。

• 递归计算阶乘

int factorial(int n)
{
    if (n==0||n==1)
        return 1;
    else
        return n*factorial(n-1);
}

int main()
{
    int x=factorial(10);
    printf("计算完成");
}

• 递归计算阶乘裴波那契数列

int Fib(int n)
{
    if (n==0)
        return 0;
    else if(n==1)
        return 1;
    else
        return Fib(n-1)+Fib(n-2)
}

int main()
{
    int x=Fib(4);
    printf("计算完成");
}

• 缺点

  太多层递归可能会导致栈溢出，或者包含很多重复的计算，浪费大量的时间时间。