串
1.定义
即是字符串,是由零个或者多个字符组成的有限序列。一般记为S=‘a1a2a3…an’(n≥0)。其中S是串名,单引号括起来的字符序列是串的值,其中ai可以是字母、数字或其他字符。
实际上,串是一种特殊的线性表,数据元素之间呈线性关系,只不过,串的数据对象限制为了字符集(中文字符、英文字符、数字字符、标点字符等),二串的基本操作,如增删改查等通常也是以子串作为操作对象。
串中任意个连续的字符组成的子序列
包含子串的串
字符在串中的序号
子串的第一个字符在主串中的位置
2.串的基本操作
- StrAssign(&T,chars);赋值操作,把串T赋值为chars
- StrCopy(&T,S);复制操作, 把串S复制得到串T
- StrEmpty(S);判空操作,若S为空串则返回TRUE,否则返回FALSE
- StrLength(S):求串长,返回串S的元素个数
- ClearString(&S):清空操作,将S清为空串
- DestroyString(&S):销毁串,将串S销毁并且回收存储空间
- Concat(&T,S1,S2):串联接,用T返回S1和S2联接而成的新串
- SubString(&Sub,S,pos,len):求子串。用Sub返回串S的第pos个字符起长度为len的子串
- Index(S,T):定位操作,若主串S存在于串T值相同的子串,则返回它在主串S中第一次出现的位置;否则函数值为0
- StrCompare(S,T):比较操作,若S>T,则返回值>0,若S=T,则返回值=0,若S<T,则返回值<0,
3.串的存储结构
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
#define MAXLEN 255
typedef struct
{
char ch[MAXLEN];
int length;
}SString;
typedef struct
{
char *ch;
int length;
}HString;
HString S;
S.ch = (char *)malloc(MAXLEN * sizeof(char));
S。length = 0;
|

1
2
3
4
5
| typedef struct StringNode
{
char ch;
struct StringNode *next;
}StringNode,*String;
|

1
2
3
4
5
| typedef struct StringNode
{
char ch[4];
struct StringNode *next;
}StringNode,* String;
|

4.串的基本操作
- 求子串SubString(&Sub,S,pos,len)
1
2
3
4
5
6
7
8
9
10
| bool SubString(SString &Sub,SString S,int pos,int len)
{
if(pos+len-1>S.length)
return false;
for(int i=pos;i<pos+len;i++)
Sub.ch[i-pos+1] = S.ch[i];
Sub.length = len;
return true;
}
|
1
2
3
4
5
6
7
8
9
| int StrCompare(SString S,SString T)
{
for(int i=1;i<=S.length&&i<=T.length;i++)
{
if(S.ch[i]!=T.ch[i])
retuen S.ch[i]-T.ch[i];
}
return S.length-T.length;
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
| int Index(SString S,SString T)
{
int i=1,n=StrLength,m=StrLength(T);
SString sub;
while(i<=n-m+1)
{
SubString(sub,S,i,m);
if(StrCompare(sub,T)!=0)
++i;
else return i;
}
return 0;
}
|
5.串的应用——朴素模式匹配算法

将主串中所有长度为m的子串依次与模式串对比,直到找到一个完全匹配的子串,或所有的子串都不匹配为止
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| int Index(SString S,SString T)
{
int i=1,j=1;
while(i<=Slength&&j<=T.length)
{
if(S.ch[i]==T.ch[j])
{
++i;
++j;
}
else
{
i=i-j+2;
j=1;
}
}
if(j>T.length)
return i-T.length;
else
return 0;
}
|
朴素模式匹配算法的最坏时间复杂度为O(mn)
6.串的应用——KMP匹配算法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| int Index_KMP(SString S,SString T,int next[])
{
int i=1,j=1;
while(i<=S.length&&j<=T.length)
{
if(j==0||S.ch[i]==T.ch[j])
{
++i;
++j;
}
else
j=next[j]
}
if(j>T.length)
return i-T.length;
else
return 0;
}
|
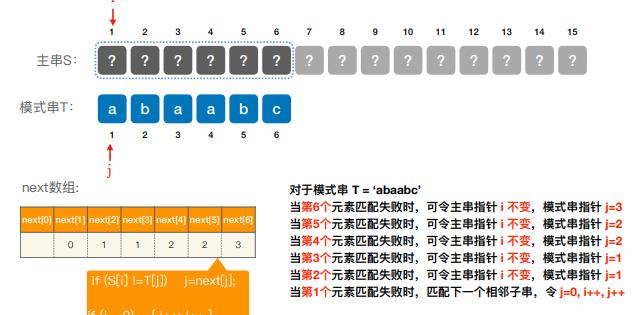
KMP算法的最坏时间复杂度是O(m+n),其中,求next数组的时间复杂度为O(m),模式匹配过程中最坏时间复杂度是O(n)
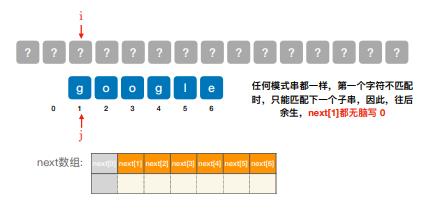
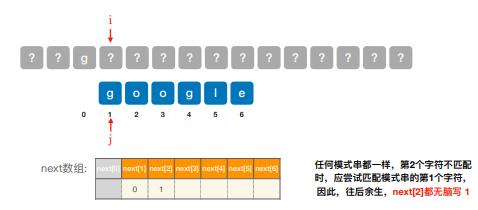
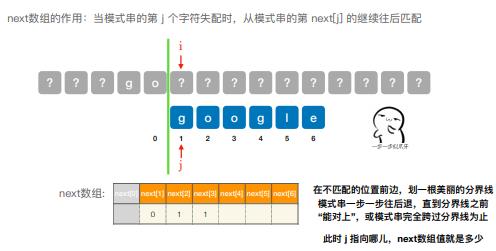
扩展: 乱码问题
在文件中,原本采用的某一套编码规则y=f(x),但当打开该文件时,你的软件以为你采用的是另外一套编码规则y=g(x),因此存在打开是乱码的情况







