树

树

1.定义

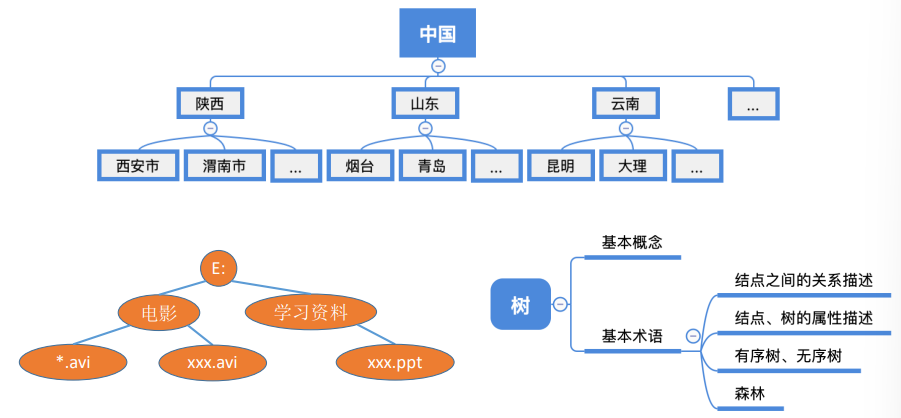
  树是一种数据结构，它是由n(n≥0)个有限节点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。当n=0时，称为空树，这是一种特殊情况。

  • 有且仅有一个特定的称为根节点
  • 没有后继的结点称为“叶子结点”
  • 有后继的结点称为“分支结点”
  • 除了根节点外，任何一个结点都有且仅有一个前驱
  • 每个结点可以有0个或多个后继
  • 当n>1时，区域结点可以分为m（m>0）个互不相交的有限集合，其中每一个集合本身又是一棵树，并且称为根节点的子树

 

2.结点之间的关系

  • 祖先结点
  • 子孙结点
  • 双亲结点（父节点）
  • 孩子结点
  • 兄弟结点
  • 堂兄弟结点

 

3.结点之间的属性

  • 路径

  只能从上到下，一个结点到另一个结点的连线

  • 路径长度

  从一个结点到另一个结点经过的边数

  • 结点的层次（深度）

  从上往下数处于第几层

  • 结点的高度

  从下往上数处于的第几层

  • 树的高度（深度）

  总共多少层

  • 结点的度

  有几个分支

  • 树的度

  各个结点的度的最大值

 

4.有序树vs无序树

  有序树从逻辑上看，树中结点的各个子树从左至右是有次序的，不能互换

  无序树从逻辑上看，树中结点的各个子树从左到右是无次序的，可以互换。

 

5.森林的定义

  森林是m（m≥0）棵互不相交的树的集合

 

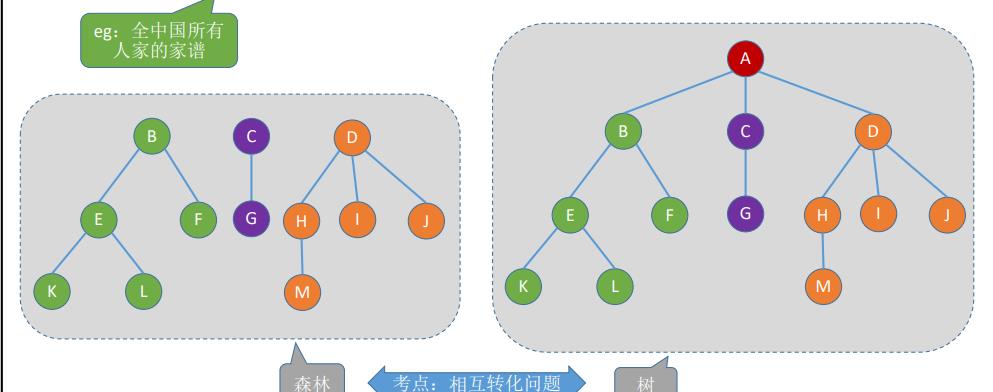
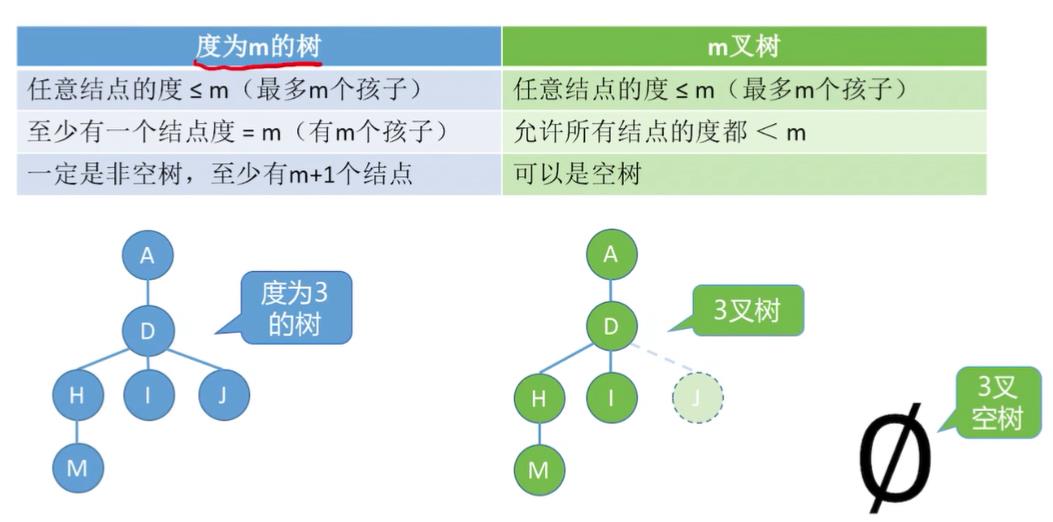
6.树的性质

  （是常见考点）

  • 结点数=总度数+1

  因为根节点的存在

  • 度为m的树与mm叉树的区别

  • 度为m的树第i层至多有m^(i-1)个结点，m叉树第i层至多有m^(i-1)个结点

  • 高度为h的m叉树至多有(m^h-1)/(m-1)个结点

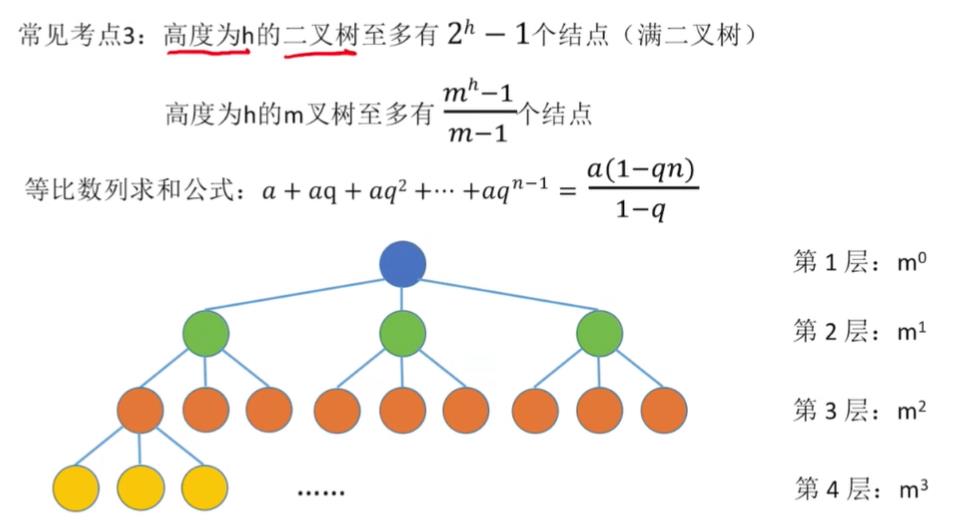
  等比数列求和：a+aq+aq^2+aq^3+……+aq^(n-1)=[a(1-q^n)]/(1-q)

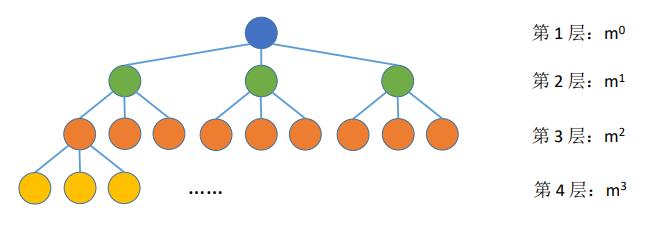
  • 高度为h的m叉树至少有h个结点，高度为h、度为m的树至少有h+m-1个结点
  • 具有n个结点的m叉树的最小高度为
 

7.二叉树的基本概念

  二叉树是n（n≥0）个结点的有限集合：

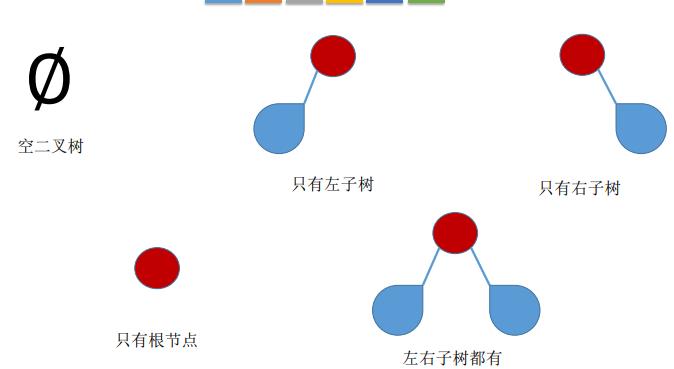
  1. 或者为空二叉树，即n = 0。
  2. 或者由一个根结点和两个互不相交的被称为根的左子树和右子树组成。左子树和右子树 又分别是一棵二叉树。

  特点：①每个结点至多只有两棵子树 ②左右子树不能颠倒（二叉树是有序树）

  • 二叉树的五种状态
  • 特殊二叉树

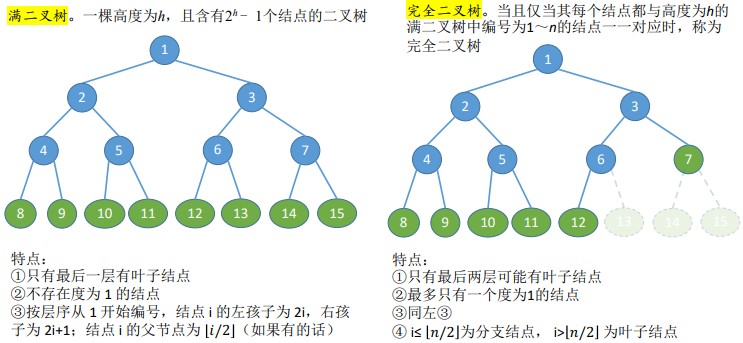
  注意：这里的完全二叉树允许度为1结点只能是左节点，如果是右节点就不是完全二叉树（完全二叉树是选择题的高频考点）

 

8.二叉树常考性质

  • 常见考点1

  设非空二叉树中度为0、1和2的结点个数分别为n0、n1和n2，则n0=n2+1（叶子结点比二分支结点多一个）

  • 常见考点2
  • 常见考点3

 

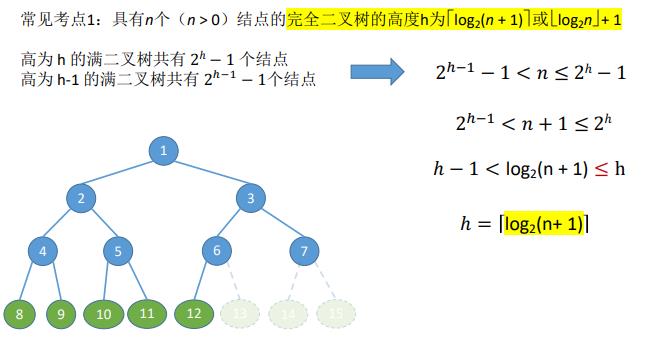
9.完全二叉树的常见考点

  • 考点1
  • 考点2

 

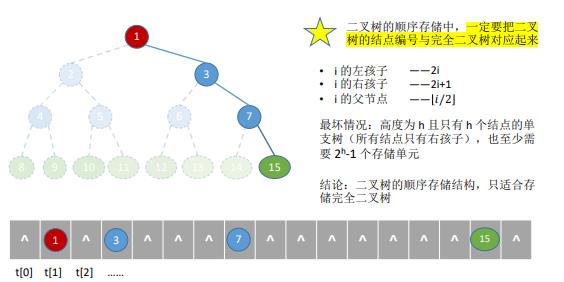
10.树的存储结构

  • 顺序存储
1
2
3
4
5
6
7
8
9
10
11
12
13
#define MaxSize 100
struct TreeNode
{
    ElemType value;
    bool idEmpty;
};

TreeNode t[MaxSize];

for(int i=0;i<MaxSize;i++)
{
    t[i].isEmpty=true;
}
  • 链式存储
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
typedef struct BiTNode
{
    ElemType data;
    struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;

//定义空树
BiTree root = NULL;

//插入根节点
root = (BiTree)malloc(sizeof(BiTNode));
root->data = {1};
root->lchild = NULL;
root->rchild = NULL;

//插入新结点
BiTNode *p = (BiTNode *)malloc(sizeof(BiTNode));
p->data = {2};
p->lchild = NULL;
p->rchild = NULL;
root->lchild = p;

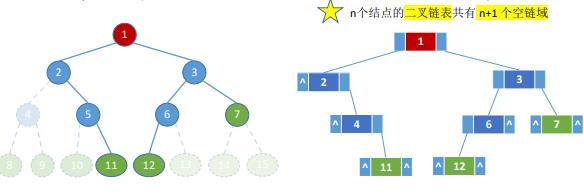
  为了方便找到父节点，我们可以在结构体中再设置一个父指针，这样子的结构体称为三叉链表

1
2
3
4
5
6
typedef struct BiTNode
{
    ElemType data;
    struct BiTNode *lchild,*rchild;
    struct BiTNode *parent;
}BiTNode,*BiTree;

 

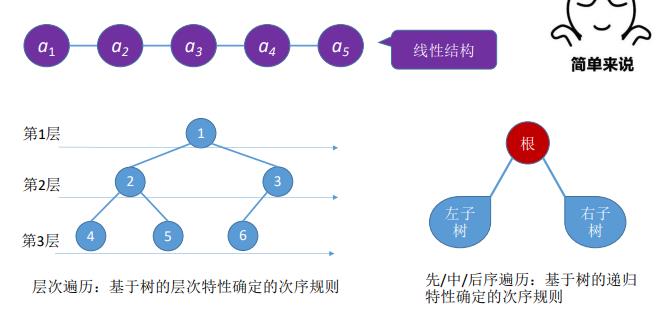
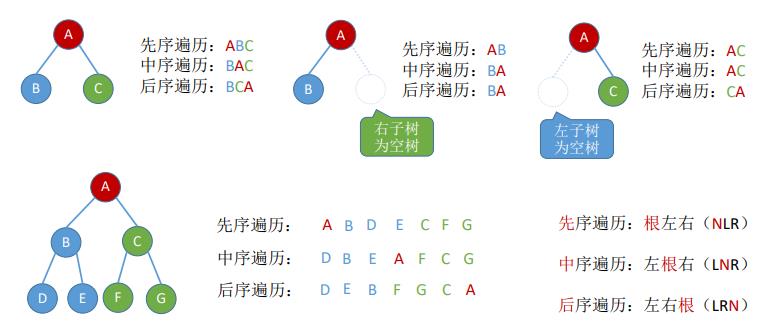
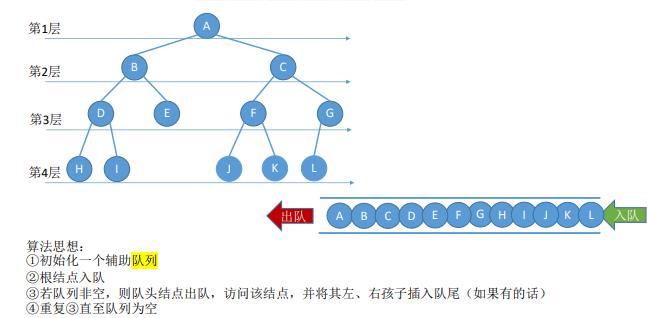
11.二叉树的遍历

  • 什么是遍历

  按照某种次序把所有的结点都访问一遍

  • 三种遍历（前、中、后）
  • 遍历代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
//先序遍历
void PreOrder(BiTree T)
{
    if(T!=NULL)
    {
        visit(T);             //访问根节点
        PreOrder(T->lchild);  //递归遍历左子树
        PreOrder(T->rchild);  //递归遍历右子树
    }
}

//中序遍历
void InOrder(BiTree T)
{
    if(T!=NULL)
    {
        InOrder(T->lchild);  //递归遍历左子树
        visit(T);             //访问根节点
        InOrder(T->rchild);  //递归遍历右子树
    }
}

//后序遍历
void PostOrder(BiTree T)
{
    if(T!=NULL)
    {
        PostOrder(T->lchild);  //递归遍历左子树
        PostOrder(T->rchild);  //递归遍历右子树        
        visit(T);             //访问根节点
    }
}
  • 求树的深度
1
2
3
4
5
6
7
8
9
10
11
12
13
int treeDepth(BiTree T)
{
    if(T == NULL)
    {
        return 0;
    }
    else
    {
        int l = treeDepth(T->lchild);
        int r = treeDepth(T->rchlid);
        return l>r ? l+1 : r+1;
    }
}
  • 层序遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
void LevelOrder(BiTREE T)
{
    LinkQueue Q;
    InitQueue(Q);
    BiTree p;
    EnQueue(Q,p);
    whlie(!IsEmpty(Q))
    {
        DeQueue(Q,p);
        visit(p);
        if(p->lchild!=NULL)
            EnQueue(Q,p->lchild);
        if(p->rchild!=NULL)
            EnQueue(Q,p->rchild);
    }
}

 

12.遍历序列构造二叉树

  • 前序+中序
  • 后序+中序
  • 层序+中序

 

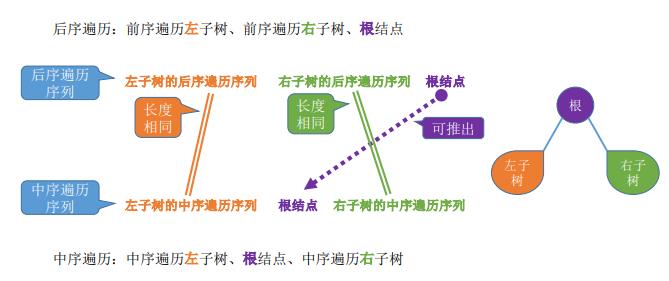
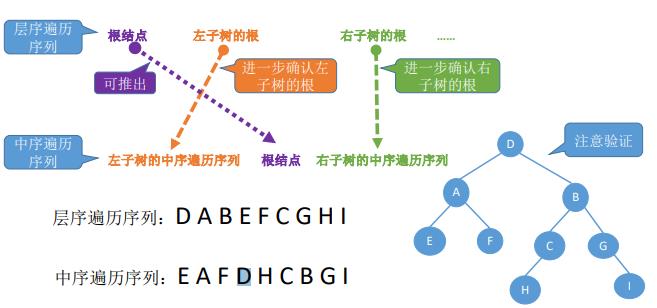
13.线索二叉树

  • 中序线索二叉树
  • 线索二叉树的存储结构
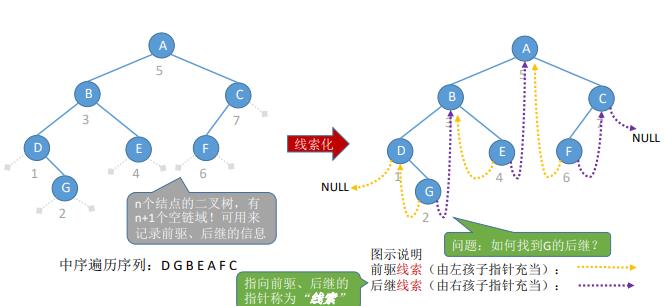
1
2
3
4
5
6
7
//线索二叉树结点
typedef struct ThreadNode
{
    ElemType data;
    struct ThreadNode *lchild,*rchild;
    int ltag,rtag;
}ThreadNode,*ThreadTree;
  • 三种线索二叉树对比

 

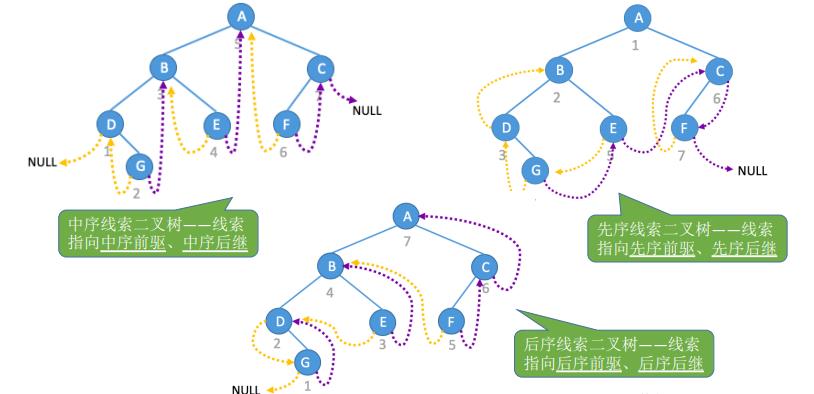
14.二叉树的线索化实现

  • 中序线索化
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
//土方法找中序前驱
void InThread(BiTree T)
{
    if(T!=NULL)
    {
        InOrder(T->lchild);  //递归遍历左子树
        visit(T);             //访问根节点
        InOrder(T->rchild);  //递归遍历右子树
    }
}

//访问结点q
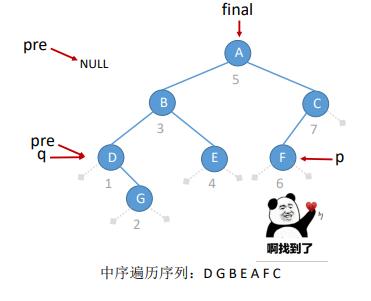
void visit(BiTNode *q)
{
    if (q==p)          //当前访问结点刚好是结点p        
        final = pre;   //找到p的前驱
    else
        pre = q;      //pre指向当前访问的结点
}

//辅助全局变量，用于查找结点判断前驱
BiTNode *p;       //p指向目标结点
BiTNode * pre=NULL;    // 指向当前访问结点的前驱
BiTNode * final=NULL;  //用于记录最终结果

 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
//中序线索化
//辅助全局变量，用于查找结点判断前驱
BiTNode * pre=NULL;    // 指向当前访问结点的前驱

//中序线索化二叉树T
void CreateInThread(ThreadTree T)
{
    pre=NULL;
    if(T!=NULL)
    {
        InThread(T);
        if(pre->rchild==NULL)
            pre->rtag=1;
    }
}

//线索二叉树结点
typedef struct ThreadNode   
{
    ElemType data;
    struct ThreadNode *lchild,*rchild;
    int ltag,rtag;
}ThreadNode,*ThreadTree;

//中序遍历二叉树
void InThread(BiTree T)
{
    if(T!=NULL)
    {
        InOrder(T->lchild);  //递归遍历左子树
        visit(T);             //访问根节点
        InOrder(T->rchild);  //递归遍历右子树
    }
}

void visit(ThreadNode *q)
{
    if(q->lchild==NULL)   //左子树为空，建立前驱线索
    {
        q->lchild=pre;
        q->ltag=1;
    }
    if(pre!=NULL&&pre->rchild==NULL)
    {
        pre->rchild=q;
        pre->rtag=1;
    }
    pre=q;
}
  • 先序线索化
  • 后序线索化

 

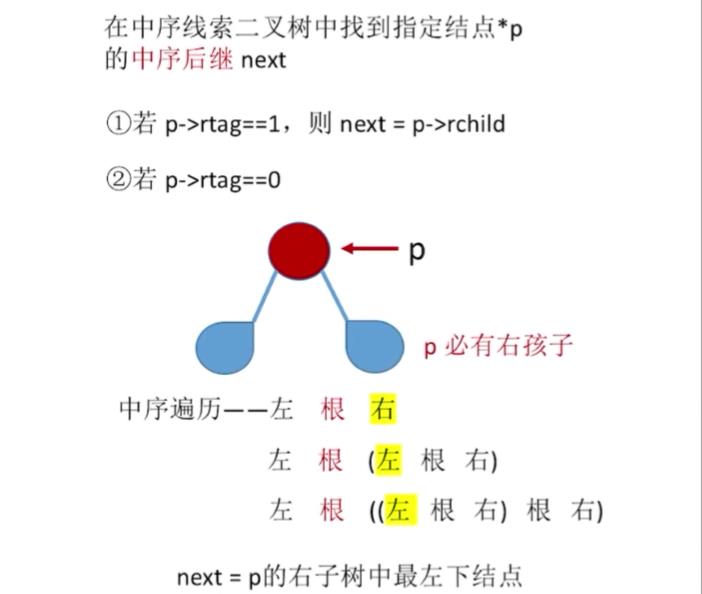
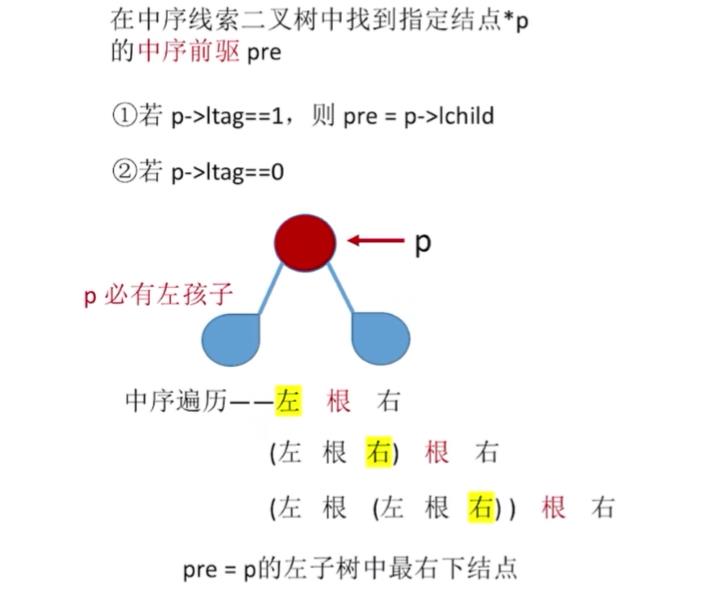
15.线索二叉树找前驱/后继

  • 中序线索二叉树查找中序后继
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
//找到以p为根的子树中，第一个被中序遍历的结点
ThreadNode *Firstnode(ThreadNode *p)
{
    //循环找到最左下结点
    while(p->ltag==0)
        p=p->lchild;
    return p;
}
//在中序线索二叉树中找到结点p的后继结点
ThreadNode *Nextnode(ThreadNode *p)
{
    //右子树最左下结点
    if(p->rtag==0)
        return Fistnode(p->rchild);
    else
        return p->rchild;
}
  • 中序线索二叉树查找中序前驱
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
//找到以p为根的子树中，最后一个被中序遍历的结点
ThreadNode *Lastnode(ThreadNode *p)
{
    //循环找到最左下结点
    while(p->rtag==0)
        p=p->rchild;
    return p;
}
//在中序线索二叉树中找到结点p的后继结点
ThreadNode *Nextnode(ThreadNode *p)
{
    //右子树最左下结点
    if(p->rtag==0)
        return Lastnode(p->lchild);
    else
        return p->lchild;
}
  • 先序线索二叉树查找先序后继
  • 先序线索二叉树查找先序前驱
  • 后序线索二叉树查找后序后继
  • 后序线索二叉树查找后序前驱

 

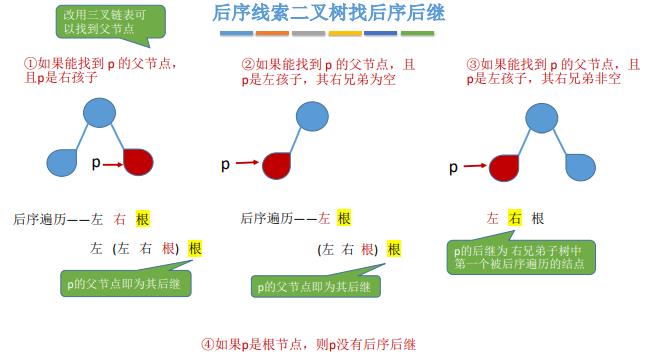
16.树的存储结构

  • 双亲表示法（顺序存储）
  • 孩子表示法（顺序+链式存储）
  • 孩子兄弟表示法（链式存储）
  • 转化问题

 

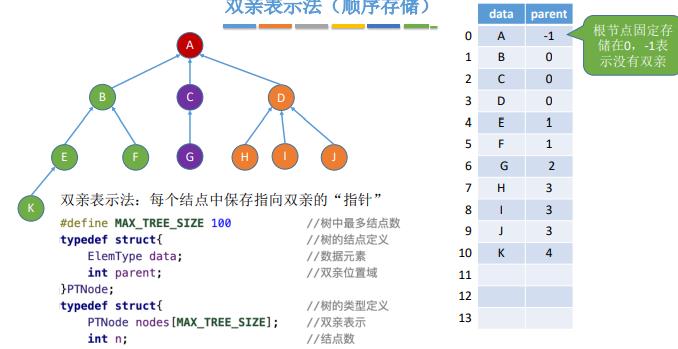
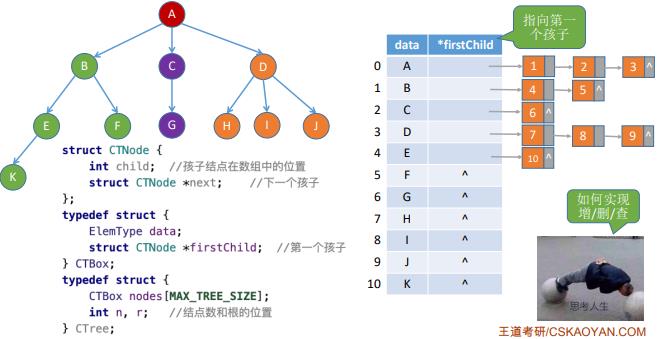
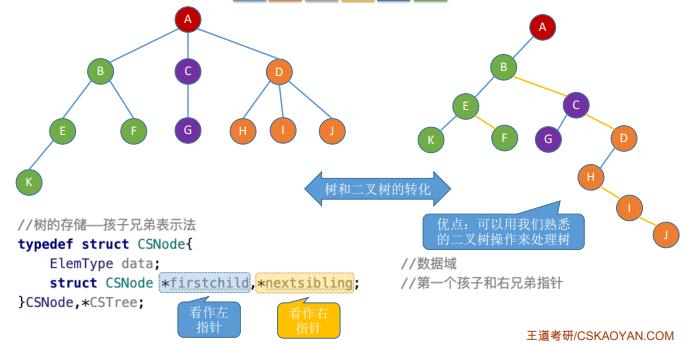
17.树的遍历

  • 先根遍历
  • 后根遍历
  • 层次遍历

 

18.森林的遍历

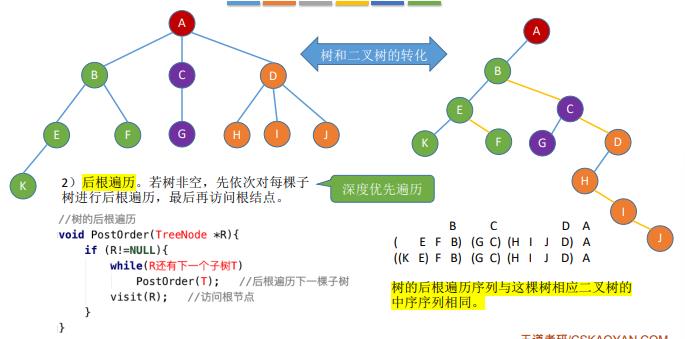
  • 先序遍历
  • 中序遍历

 

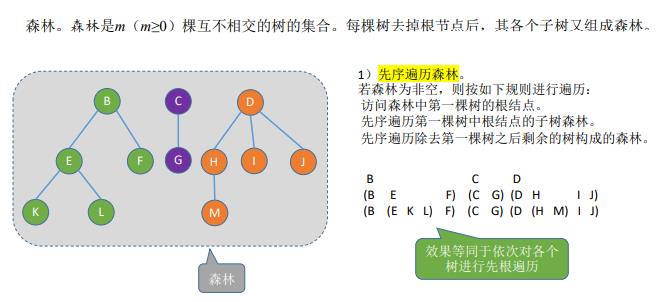
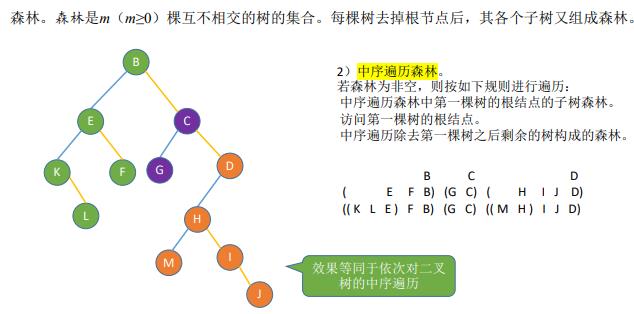
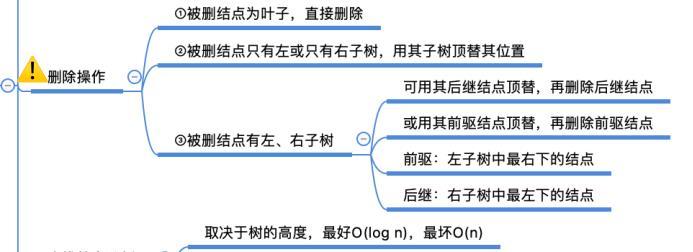
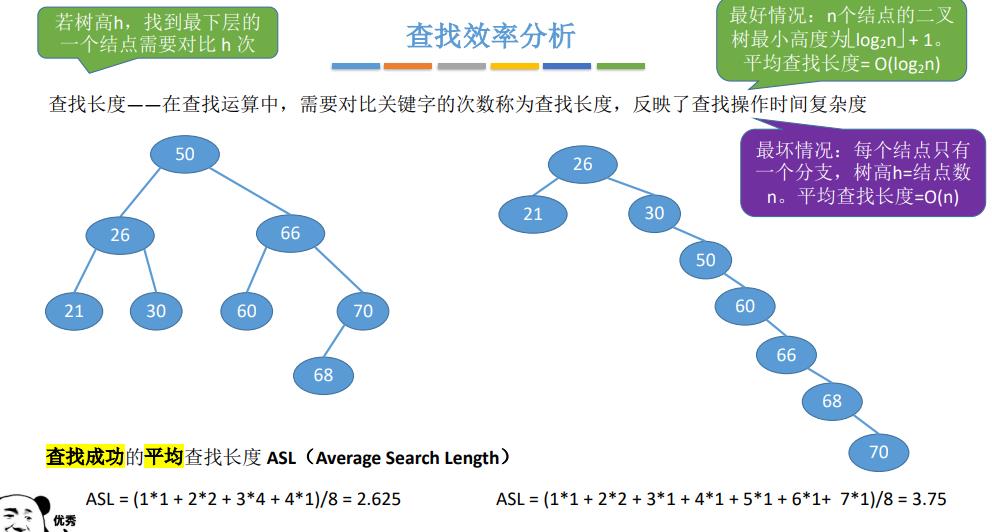
19.二叉排序树

   二叉排序数，又称二叉查找树（BST），一棵二叉树或者空二叉树，或者是具有如下性质的二叉树；

  左子树上所有结点的关键字均小于根节点的关键字；

  右子树上所有结点的关键字均大于根节点的关键字。

  左子树和右子树由各是一棵二叉排序树。

  • 二叉排序树的查找
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
//正常实现思路
BSTNode *BST_Search(BSTree T,int key)
{
    while(T!=NULL&&key!=T->key)
    {
        if(key<T->key)
            T=T->lchild;
        else
            T=T->rchild;
    }
    return T;
}

//递归实现思路
BSTNode *BSTSearch(BSTree T,int key)
{
    if(T==NULL)
        return NULL;
    if(key==T->key)
        return T;
    else if(key < T->key)
        return BSTSearch(T->lchild,key);
    else
        return BSTSearch(T->rchild,key);
}
  • 二叉排序树的插入
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
//递归实现思路
BSTNode *BST_Insert(BSTree &T,int key)
{
    if(T==NULL)
    {
        T=(BSTree)malloc(sizeof(BSTNode));
        T->key=k;
        T->lchild=T->rchild=NULL;
        return 1;
    }
    else if(key==T->key)
        return 0;
    else if(key < T->key)
        return BST_Insert(T->lchild,key);
    else
        return BST_Insert(T->rchild,key);
}
  • 二叉排序树的构造
1
2
3
4
5
6
7
8
9
10
void Creat_BST(BSTree &T,int str[],int n)
{
    T=NULL;
    int i=0;
    while(i<n)
    {
        BST_Insert(T,str[i]);
        i++;
    }
}
  • 二叉排序树的删除
  • 查找效率计算

 

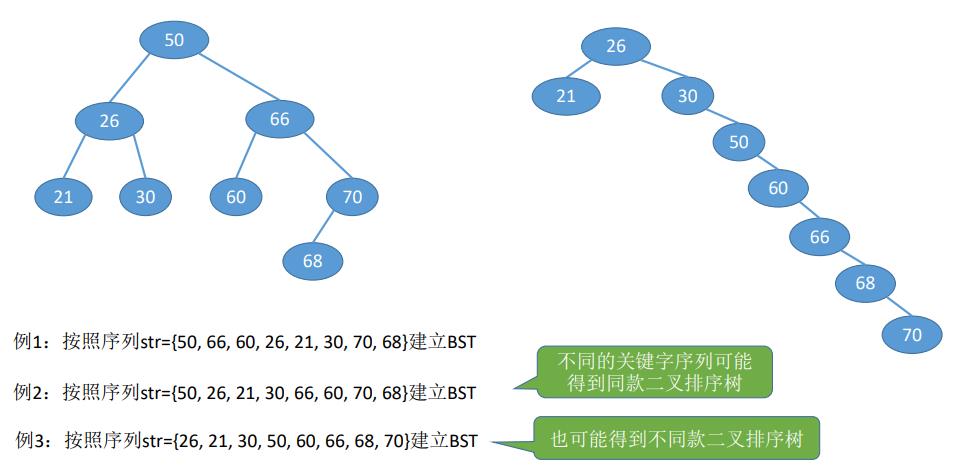
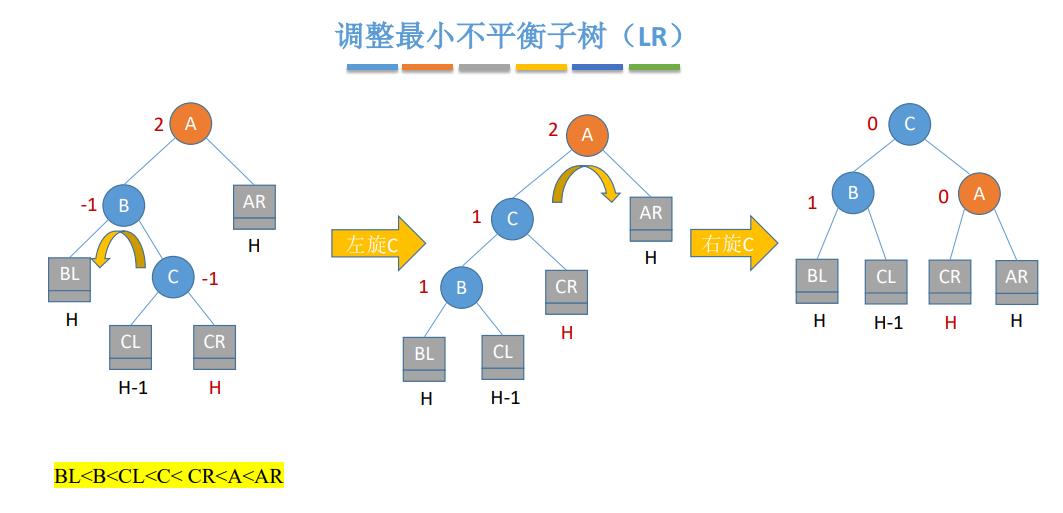
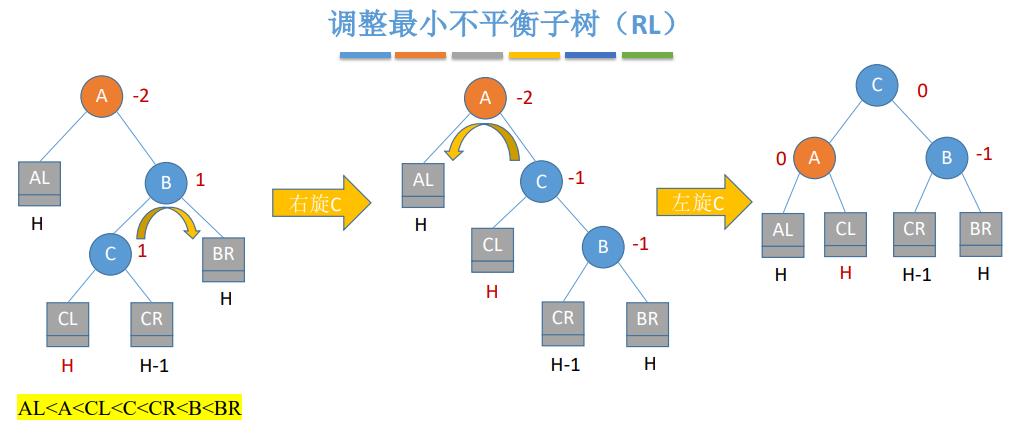
20.平衡二叉树

  • 定义

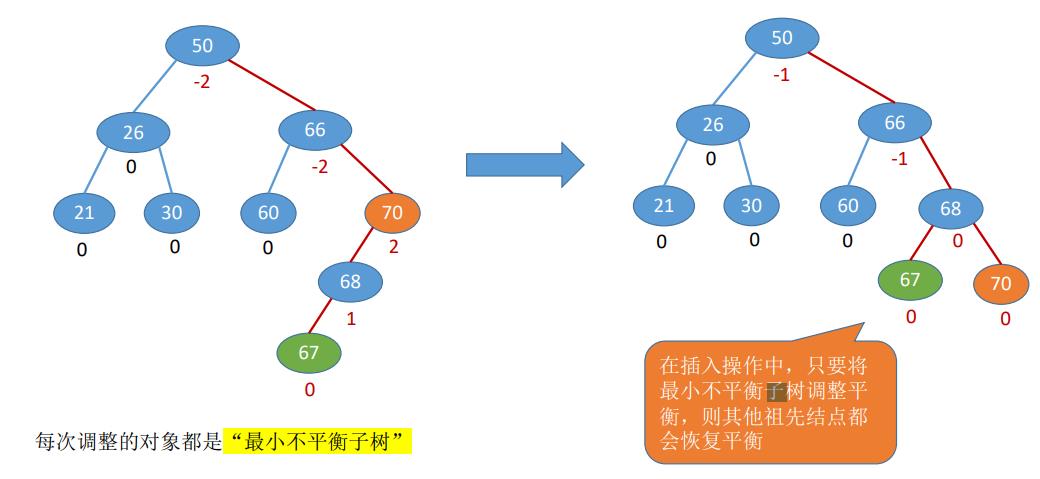
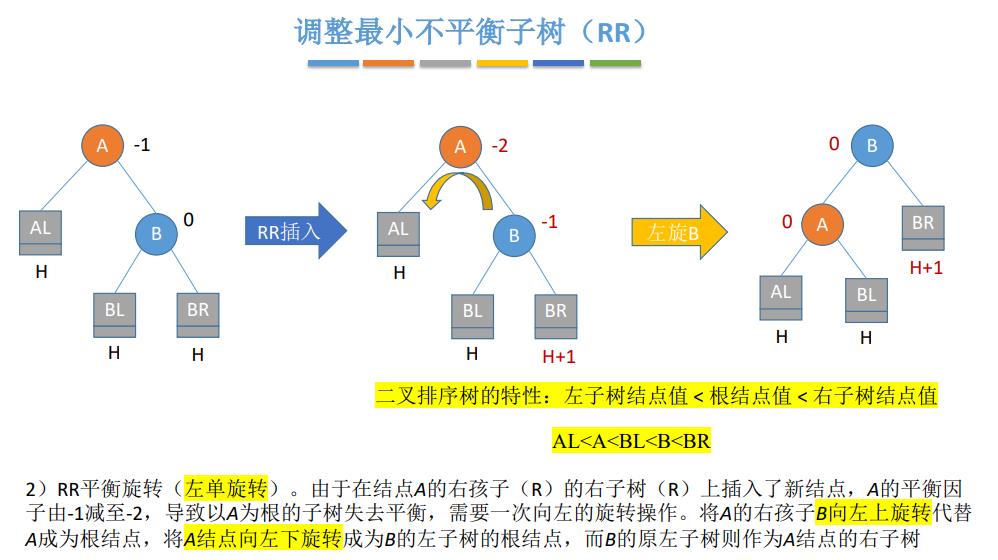
  平衡二叉树，简称平衡树（AVL树）——树上任一结点的左子树和右子树的高度之差不超过1

  结点的平衡因子=左子树高-右子树高

1
2
3
4
5
6
7
//平衡二叉树结点
typedef struct AVLNode
{
    int key;
    int balance;
    struct AVLNode *lchild,*rchild;
}AVLNode,*AVLTree;
  • 平衡二叉树的插入
  • 调制不平衡树的四种情况
  • 查找效率分析

 

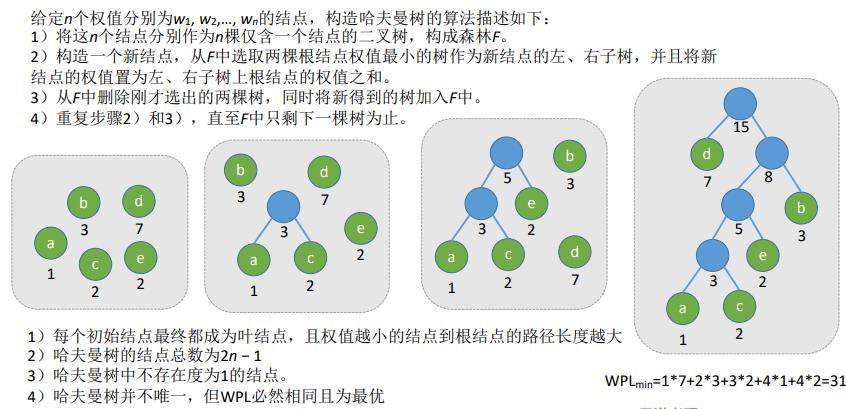
21.哈夫曼树

  • 带权路径长度

  结点的权：有某种现实含义的数值

  接单的带权路径长度：从树的根到该结点的路径长度（经过的边数）与该接单上权值的乘积

  树的带权路径长度：树中所有叶接单的带权路径长度之和（WPL）

  • 哈夫曼树的定义

  在含有n个带权叶结点的二叉树中，其中带权路径长度（WPL）最小的二叉树称为哈夫曼树，也称为最优二叉树，是图中红色框出的部分

  • 哈夫曼树的构造
  • 哈夫曼编码
  • 编码类型
数据结构学习笔记
树
https://one-null-pointer.github.io/2022/10/22/数据结构七/
Author
liaoyue
Posted on
October 22, 2022
传送口