查找
查找
1.基本概念
查找:在数据集合中寻找到满足某种条件的数据元素的过程称之为查找
查找表(查找结构):用于查找的数据集合合称为查找表,它是由同一类型的数据元素(或记录)组成
关键字:数据元素汇总唯一识别该元素的某个数据项的值,使用基于关键字的查找,查找结果应该是唯一的
查找长度:在查找运算中,需要对比关键字的次数称为查找长度
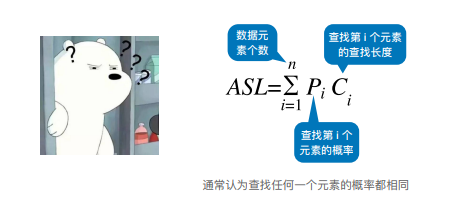
平均查找长度(ASL):所有查找过程中进行关键字的比较次数的平均值
2.顺序查找
顺序查找有称为“线性查找”,通常用于线性表中,算法的中心思想就是从到到位挨个进行查找
1 | |
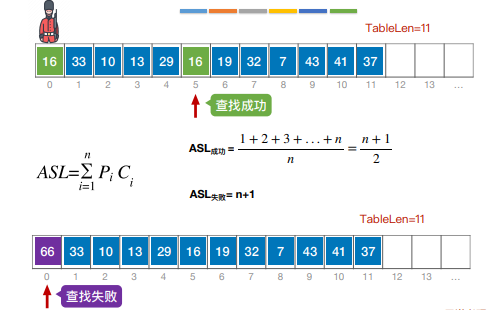
有序的排列有利于提高查找的效率

3.折半查找
折半查找有称为“二分查找”,仅适用于有序的顺序表
1 | |
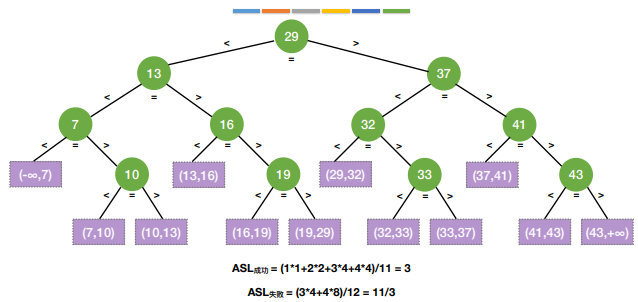
注:如果当前low和high之间有偶数个元素,则 mid 分隔后,左半部分⽐右半部分少⼀个元素,并且折半查找的判定树一定是平衡二叉树,只有最下面一层是不满的
4.分块查找
分块查找有称索引顺序查找,实现通过索引表中确定待查记录所属的分块(可顺序、可折半),然后在快内顺序查找
“索引表”中保存每个分 块的最⼤关键字和分块 的存储区间
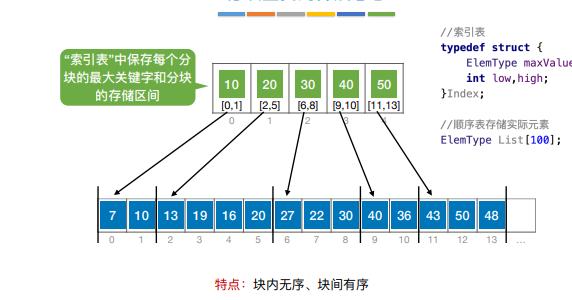
1 | |
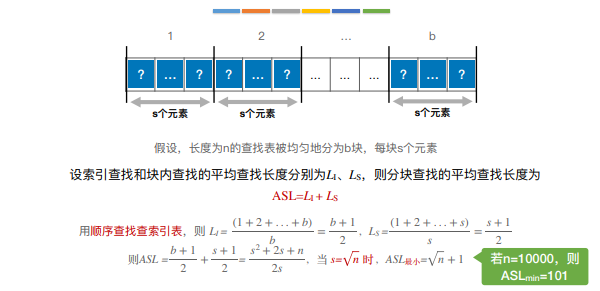

注:常考的效率为顺序查找索引表
5.B树
一般来说比较注重的是B树的性质、插入、删除、查找等相关内容
1 | |
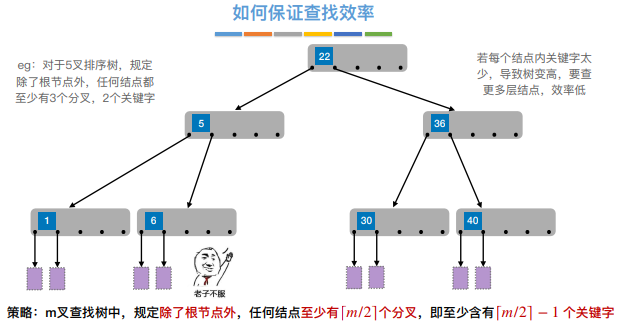
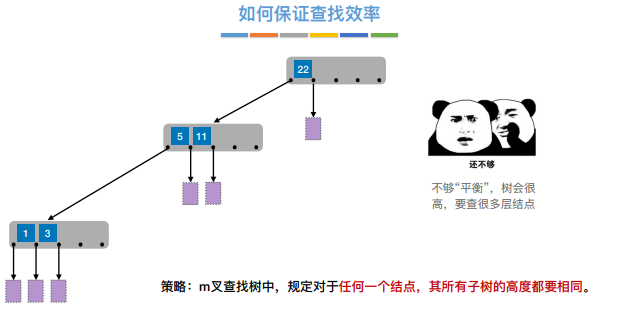
B树,⼜称多路平衡查找树,B树中所有结点的孩⼦个数的最⼤值称为B树的阶,通常⽤m表示。⼀棵m阶B树 或为空树,或为满⾜如下特性的m叉树:
1)树中每个结点⾄多有m棵⼦树,即⾄多含有m-1个关键字
2)若根结点不是终端结点,则⾄少有两棵⼦树
3)除根结点外的所有⾮叶结点⾄少有⌈m/2⌉棵⼦树,即⾄少含有 ⌈m/2⌉-1个关键字
4)所有的叶结点都出现在同⼀层次上,并且不带信息(可以视为外部结点或类似于折半查找判定树的查找失 败结点,实际上这些结点不存在,指向这些结点的指针为空)
5)所有⾮叶结点的结构如下:
| n | p 0 | k1 | p1 | k2 | p2 | … | kn | pn |
|---|
其中,Ki(i = 1, 2,…, n)为结点的关键字,且满⾜K1 < K2 <…< Kn;Pi(i = 0, 1,…, n)为指向⼦树根结点 的指针,且指针Pi-1所指⼦树中所有结点的关键字均⼩于Ki,Pi所指⼦树中所有结点的关键字均⼤于Ki,n(⌈m/2⌉- 1≤n≤m - 1)为结点中关键字的个数。
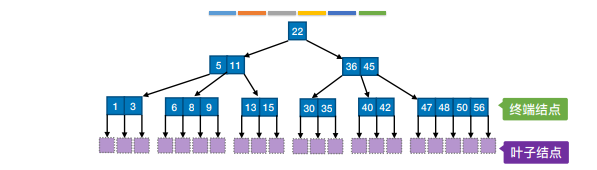
1) 根节点的⼦树数∈[2, m],关键字数∈[1, m-1]。 其他结点的⼦树数∈[⌈m/2⌉ , m];关键字数∈[ ⌈m/2⌉-1, m-1]
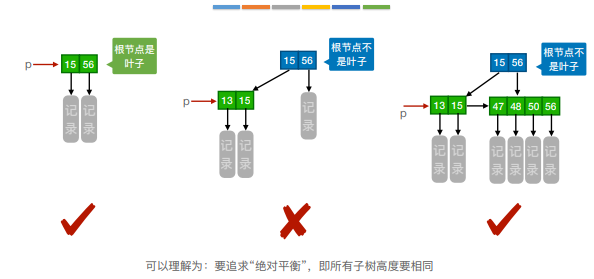
2)对任⼀结点,其所有⼦树⾼度都相同
3)关键字的值:⼦树0<关键字1<⼦树1<关键字2<⼦树2<…. (类⽐⼆叉查找树 左<中<右)
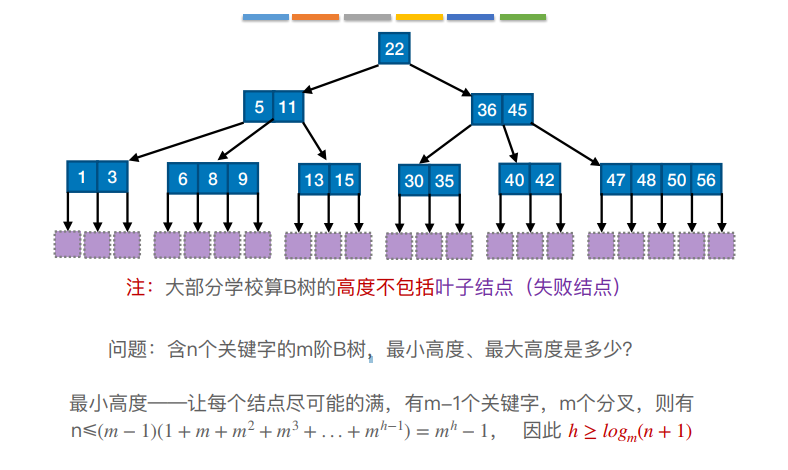
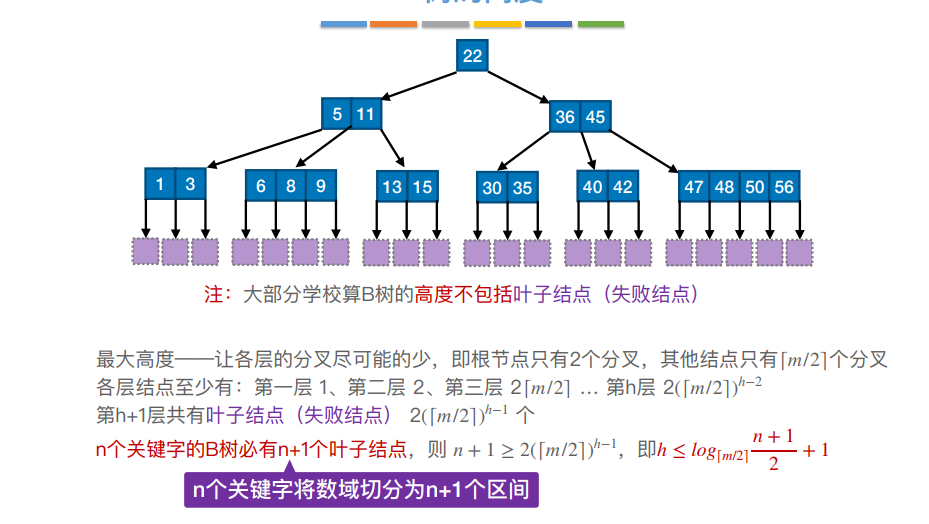
6.B树的插入和删除
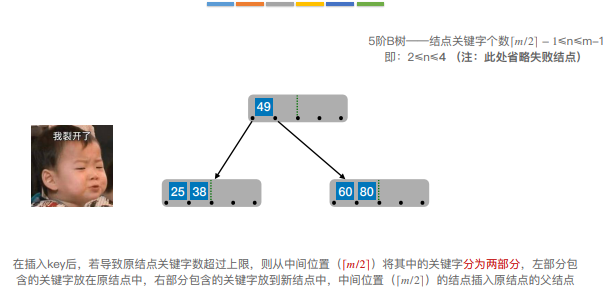
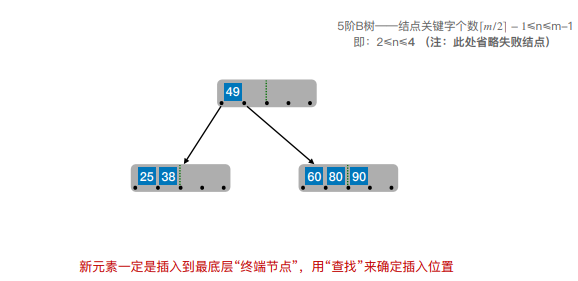
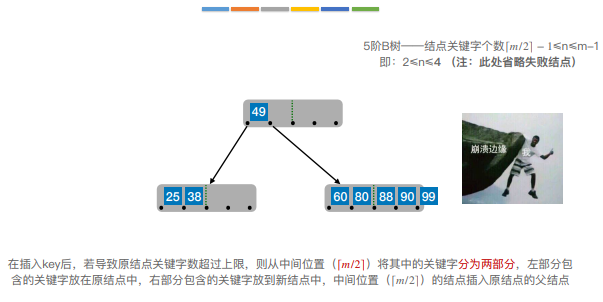


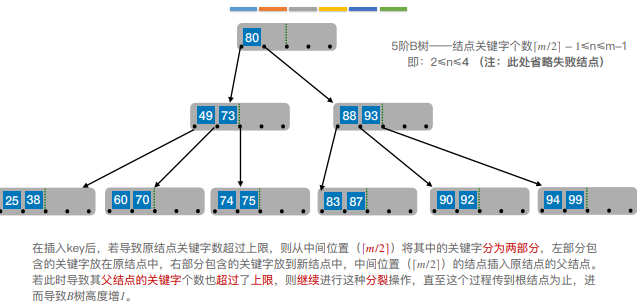

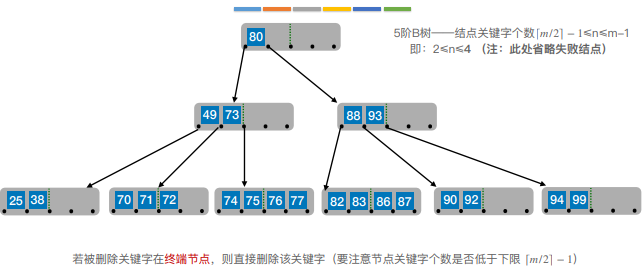

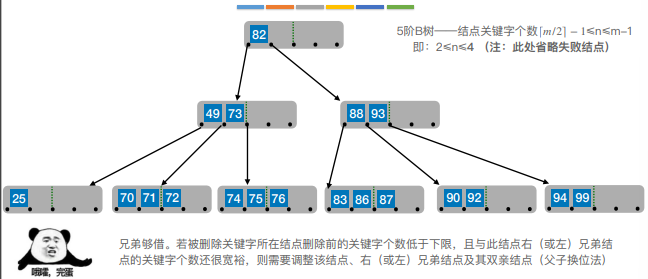


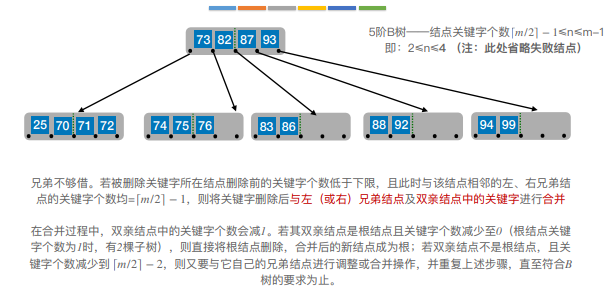
7.B+树
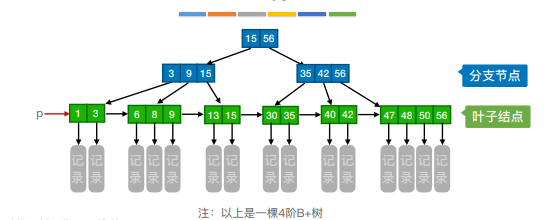
一般只要求掌握概念⼀棵m阶的B+树需满⾜下列条件:
1)每个分⽀结点最多有m棵⼦树(孩⼦结点)
2)⾮叶根结点⾄少有两棵⼦树,其他每个分⽀结点⾄少有⌈m/2⌉棵⼦树。
3)结点的⼦树个数与关键字个数相等。
4)所有叶结点包含全部关键字及指向相应记录的指针,叶结点中将关键字按⼤⼩顺序排列,并且相邻叶结点按⼤⼩顺序相互链接起来。
5)所有分⽀结点中仅包含它的各个⼦结点中关键字的最⼤值及指向其⼦结点的指针。

8.散列查找
散列表,又称哈希表,是一种数据结构,特点是:数据元素的关键字与其存储地址直接相关

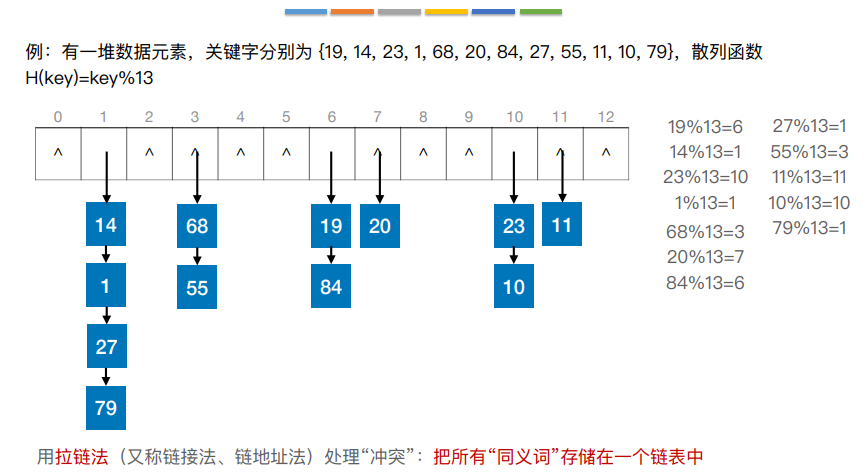

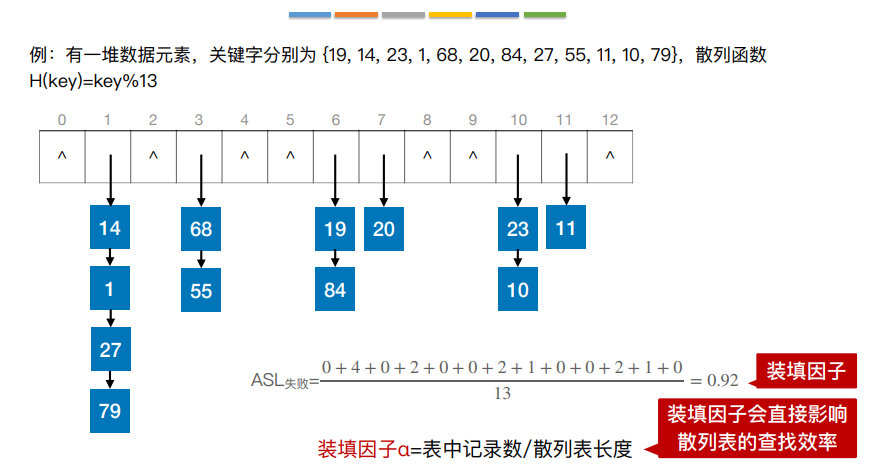
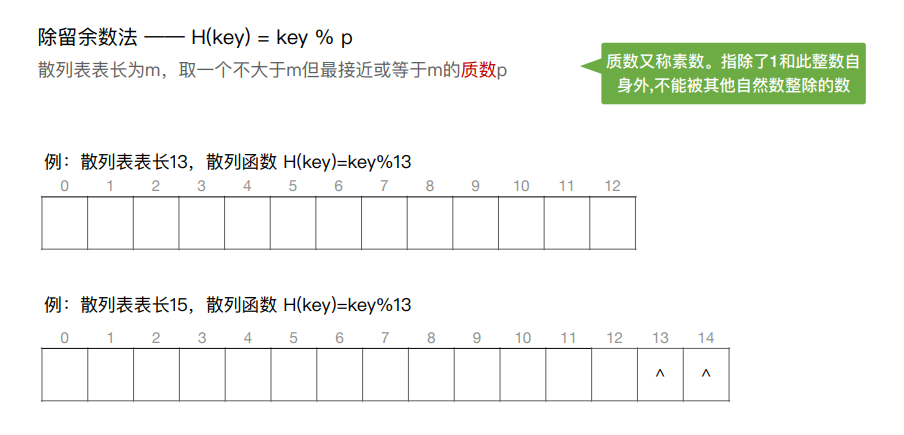



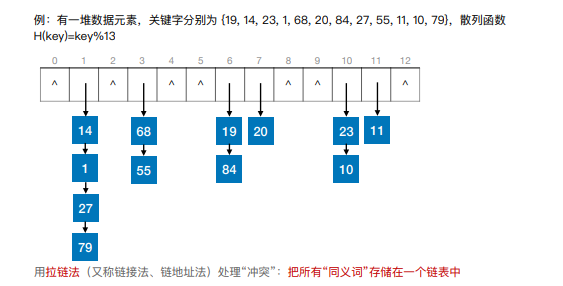
9.散列查找处理冲突方法——拉链法
10.散列查找处理冲突方法——开放定址法





⾮重点⼩坑:散列表⻓度m必须是⼀个可以表示成4j + 3的素数,才能探测到所有位置

11.散列查找处理冲突方法——再散列法
一般而言不经常考,理解即可
