排序
1.基本概念
排序:就重新排列表汇总的元素,使表中的元素满足按关键字有序的过程
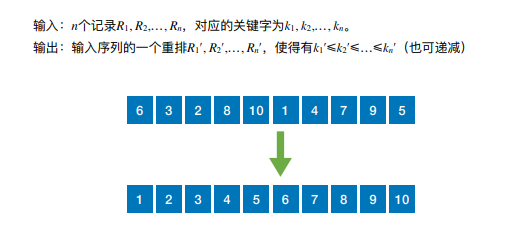
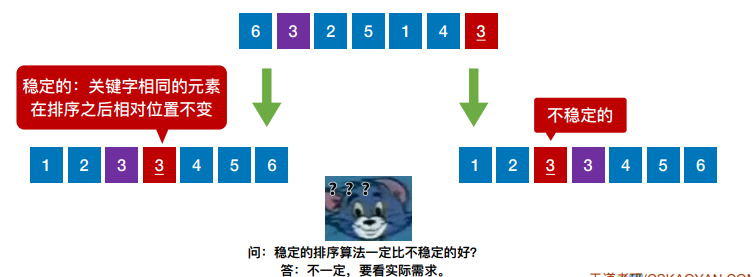
算法的稳定性,若待排序表中有两个元素Ri和Rj,其对应的关键字相同即keyi = keyj,且在排序 前Ri在Rj的前⾯,若使⽤某⼀排序算法排序后,Ri仍然在Rj的前⾯,则称这个排序算法是稳定 的,否则称排序算法是不稳定的
2.插入排序
每次将一个待排序的记录按其关键字大小插入到前面已经排好序的子序列中,直到全部记录插入完成
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
|
void InsertSort(int A[],int n)
{
int i,j,temp;
for(i=1;i<n;i++)
{
if(A[i]<A[i-1])
{
temp=A[i];
for(j=i-1;j>=0&& A[j]>temp;--j)
A[j+1]=A[j];
A[j+1]=temp;
}
}
}
void InsertSort(int A[],int n)
{
int i,j;
for(i=2;i<n;i++)
{
if(A[i]<A[i-1])
{
A[0]=A[i];
for(j=i-1;A[0]<A[j];--j)
A[j+1]=A[j];
A[j+1]=A[0];
}
}
}
|



1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
void InsertSort(int A[],int n)
{
int i,j,low,high,mid;
for(i=2;i<n;i++)
{
A[0]=A[i];
low=1;
high=i-1;
while(low<=high)
{
mid=(low+high)/2;
if(A[mid]>A[0])
high=mid-1;
else
low=mid+1;
}
for(j=i-1;j>=high+1;--j)
A[j+1]=A[j];
A[high+1]=A[0];
}
}
|
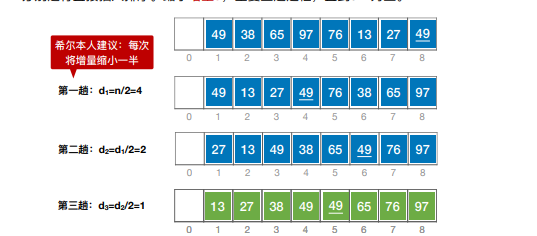
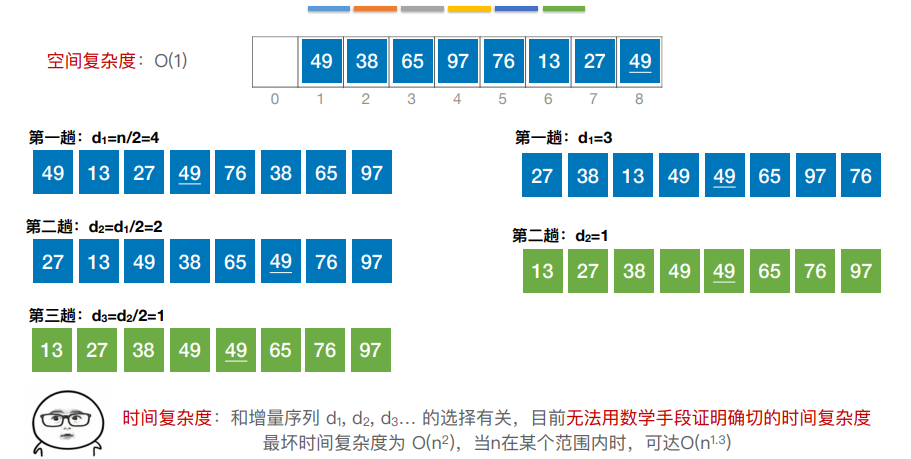
3.希尔排序
希尔排序:先将待排序表分割成若⼲形如 L[i, i + d, i + 2d,…, i + kd] 的“特殊”⼦表,对各个⼦表 分别进⾏直接插⼊排序。缩⼩增量d,重复上述过程,直到d=1为⽌。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
void ShellSort(int A[],int n)
{
int d,i,j;
for(d=d/2;d>=1;d=d/2)
{
for(i=d+1;i<=n;++i)
{
if(A[i]<A[i-d])
{
A[0]=A[i];
for(j=i-d;j>0 && A[0]<A[j];j-=d)
{
A[j+d]=A[j];
}
A[j+d]=A[0];
}
}
}
}
|

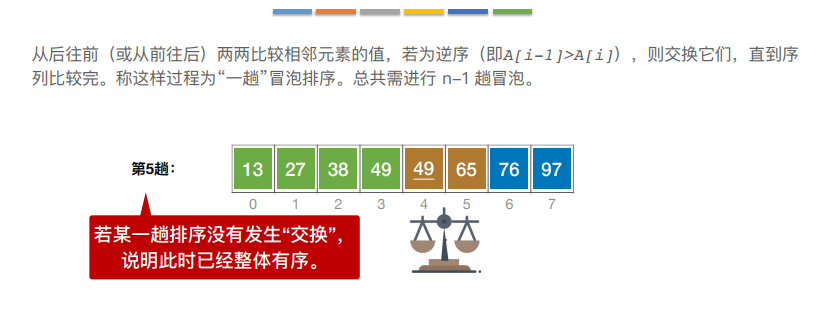
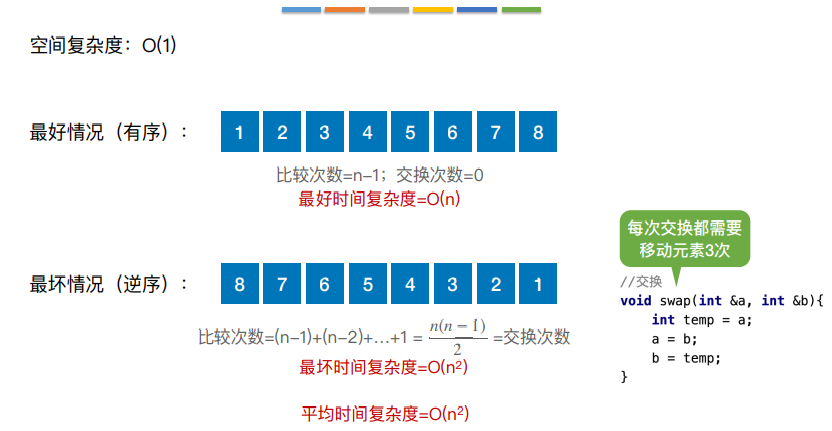
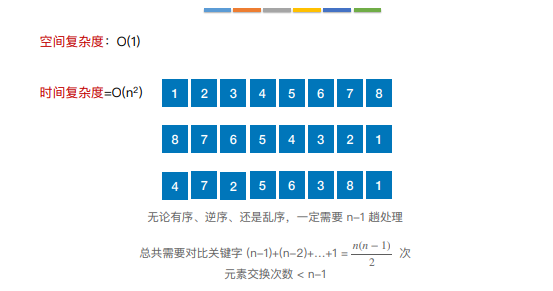
4.冒泡排序
基于“交换”的排序:根据序列中两个元素关键字的⽐较结果来对换这两个记录在序列中的位置
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
|
void swap(int &a,int &b)
{
int temp = a;
a = b;
b= temp;
}
void BubbleSort(int A[],int n)
{
for(int i=0;i<n-1;i++)
{
bool flag=false;
for(int j=n-1;j>i;j--)
{
if(A[j-1]>A[j])
{
swap(A[j-1],A[j]);
flag=ture
}
}
if(flag==false)
return;
}
}
|
5.快速排序(重点)
在待排序表L[1…n]中任取⼀个元素pivot作为枢轴(或基准,通常取⾸元素),通过⼀趟排序将待排序表划 分为独⽴的两部分L[1…k-1]和L[k+1…n],使得L[1…k-1]中的所有元素⼩于pivot,L[k+1…n]中的所有元素⼤于等于 pivot,则pivot放在了其最终位置L(k)上,这个过程称为⼀次“划分”。然后分别递归地对两个⼦表重复上述过程,直⾄ 每部分内只有⼀个元素或空为⽌,即所有元素放在了其最终位置上。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
int Partiton(int A[],int low,int high)
{
int pivot=A[low];
while(low<high)
{
while(low<high&&A[high]>=pivot)
--high;
A[low]=A[high];
while(low<high&&A[low]<=pivot)
++low;
A[high]=A[low];
}
A[low]=pivot;
return low;
}
void QuickSort(int A[],int low,int high)
{
if(low<high)
{
int pivotpos=Partiton(A,low,high);
QuickSort(int A[],int low,int high);
QuickSort(int A[],int low,int high)
}
}
|


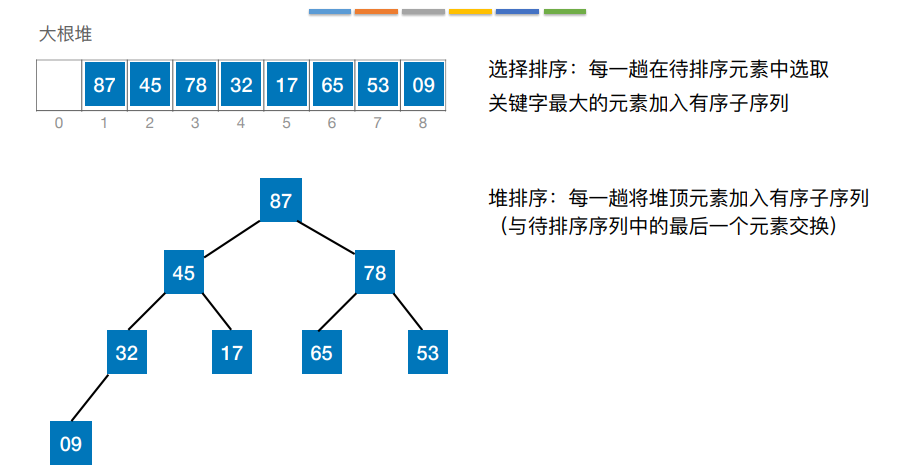
6.简单选择排序
每⼀趟在待排序元素中选取关键字最⼩的元素加⼊有序⼦序列
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
void SelectSort(int A[],int n)
{
for(int i=0;i<n-1;i++)
{
int min=1;
for(int j=i+1;j<n;j++)
{
if(A[j]<A[min])
min=j;
}
if(min!=i)
swap([A[i],A[min]);
}
}
|
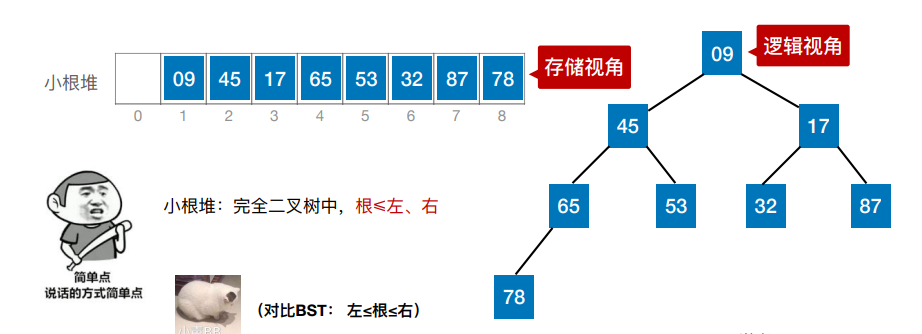
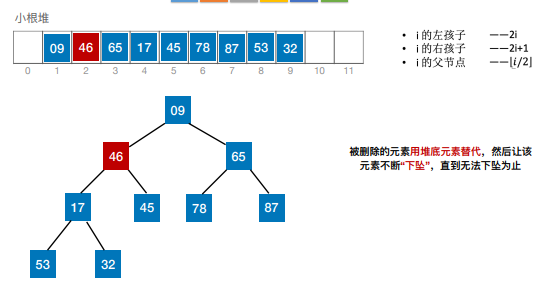
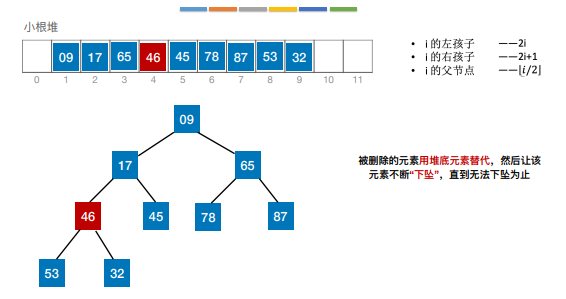
7.堆排序
若n个关键字序列L[1…n] 满⾜下⾯某⼀条性质,则称为堆(Heap):
① 若满⾜:L(i)≥L(2i)且L(i)≥L(2i+1) (1 ≤ i ≤n/2 )—— ⼤根堆(⼤顶堆)

② 若满⾜:L(i)≤L(2i)且L(i)≤L(2i+1) (1 ≤ i ≤n/2 )—— ⼩根堆(⼩顶堆)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
void BuildMaxHeap(int A[],int len)
{
for(int i=len/2;i>0;i--)
HeadAdjust(A,i,len);
}
void HeadAdjust(int A[],int k,int len)
{
A[0]=A[k];
for(int i=2*k;i<=len;i*=2)
{
if(i<len&&A[i]<A[i+1])
i++;
if(A[0]>=A[i])
break;
else
{
A[k]=A[i];
k=i;
}
}
A[k]=A[0];
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
void BuildMaxHeap(int A[],int len)
void HeadAdjust(int A[],int k,int len)
void HeapSort(int A[],int len)
{
BuildMaxHeap(A,len);
for(int i=len;i>1;i--)
{
swap(A[i],A[1]);
HeadAdjust(A,1,i-1);
}
}
|


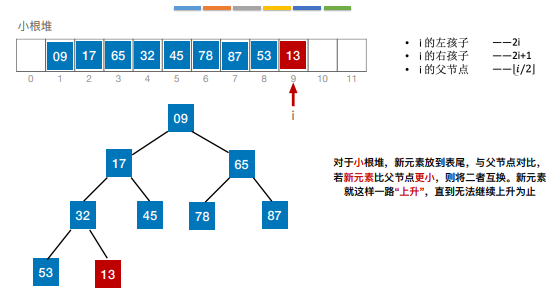
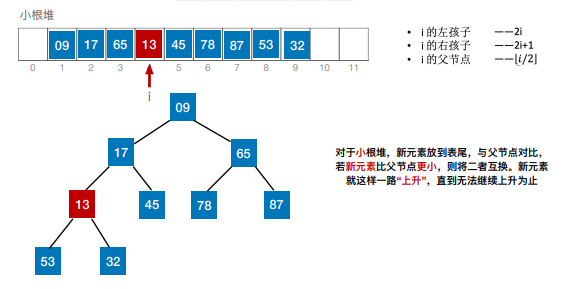
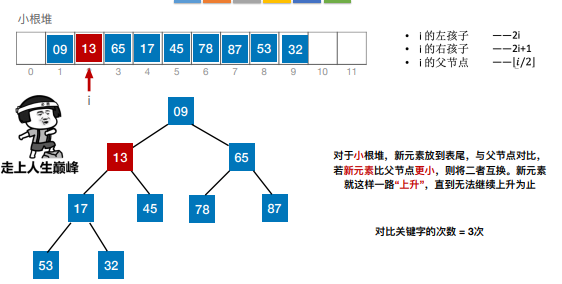


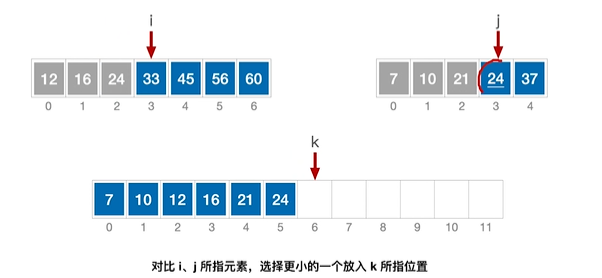
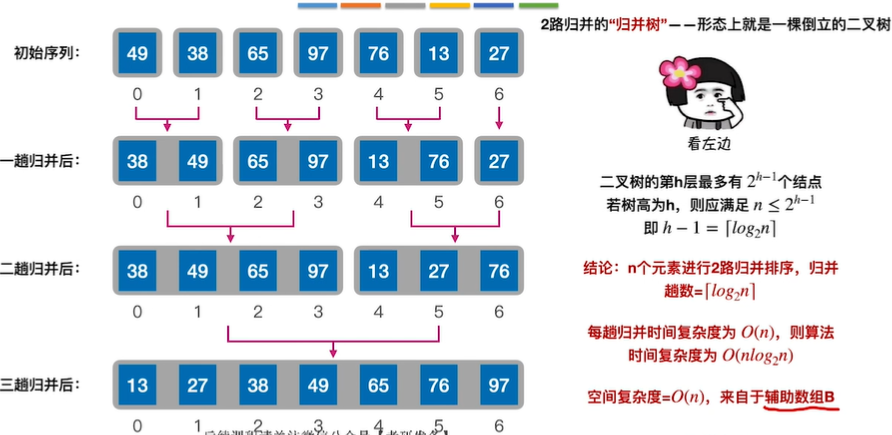
8.归并排序
归并:把两个或者多个已经有序的序列合并成一个

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
| int *B=(int *)malloc(n*sizeof(int));
void Merge(int A[],int low,int mid,int high)
{
int i,j,k;
for(k=low;k<=high;k++)
B[k]=A[k];
for(i=low,j=mid+1,k=i;i<=mid&&j<=high;k++)
{
if(B[i]<=B[j])
A[k]=B[i++];
else
A[k]=B[j++];
}
while(i<=mid)
A[k++]=B[i++];
while(j<=high)
A[k++]=B[j++];
}
void MergeSort(int A[],int low,int high)
{
if(low<high)
{
int mid=(low+high)/2;
MergeSort(A,low,mid);
MergeSort(A,mid+1,high);
Merge(A,low,mid,high);
}
}
|
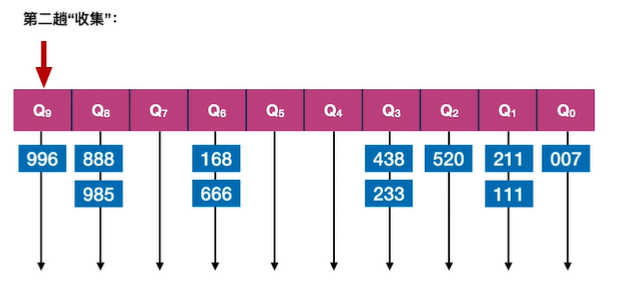
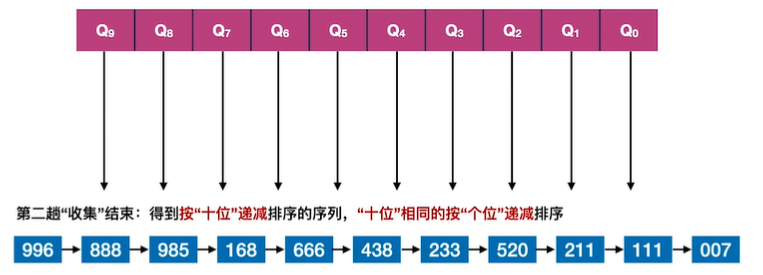
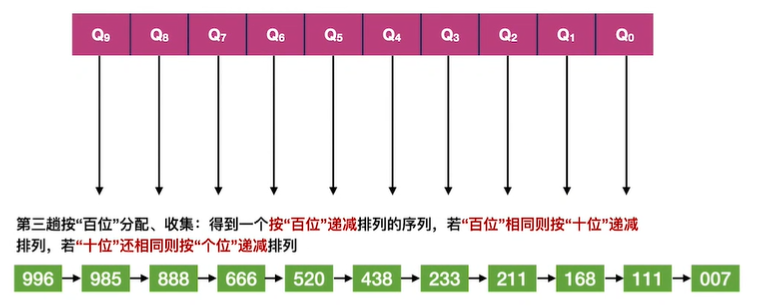
9.基数排序
假设长度为n的线性表中每个结点aj的关键字由d元组组成,其中:
0≤kij≤r-1(0≤j<n,0≤i≤d-1),r称为“基数”




1
2
3
4
5
6
7
8
9
10
| typedef struct LinkNode
{
ElemType data;
struct LinkNode *next;
}LinkNode,*LinkList;
typedef struct //链式队列
{
LinkNode *front,*rear;
}LinkQueue;
|

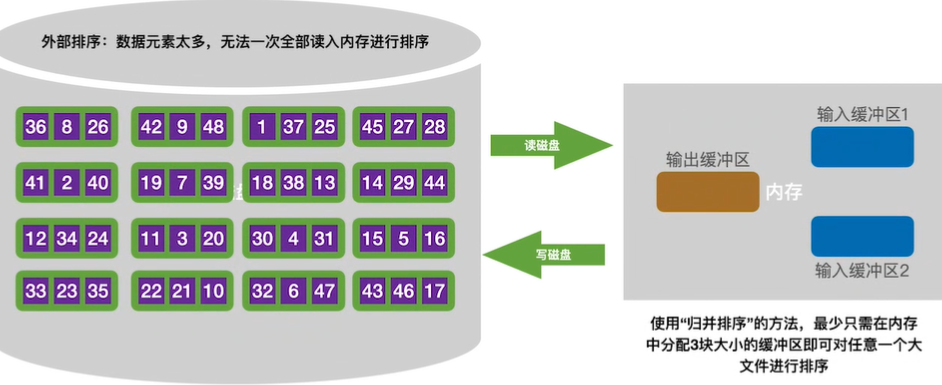
10.外部排序

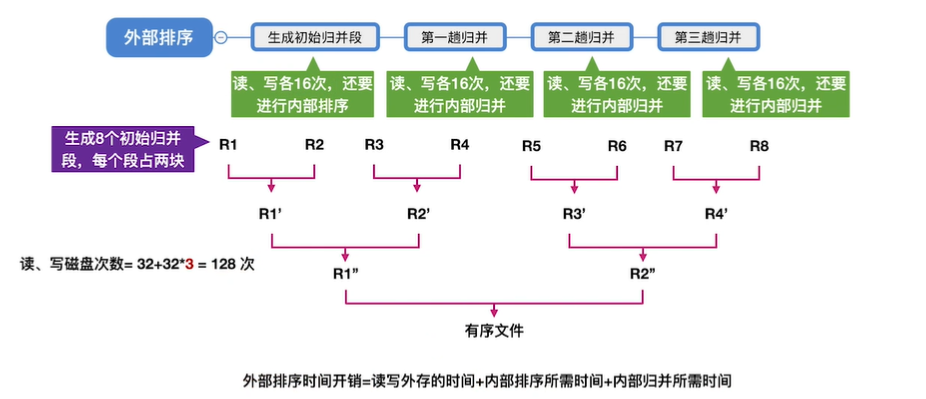

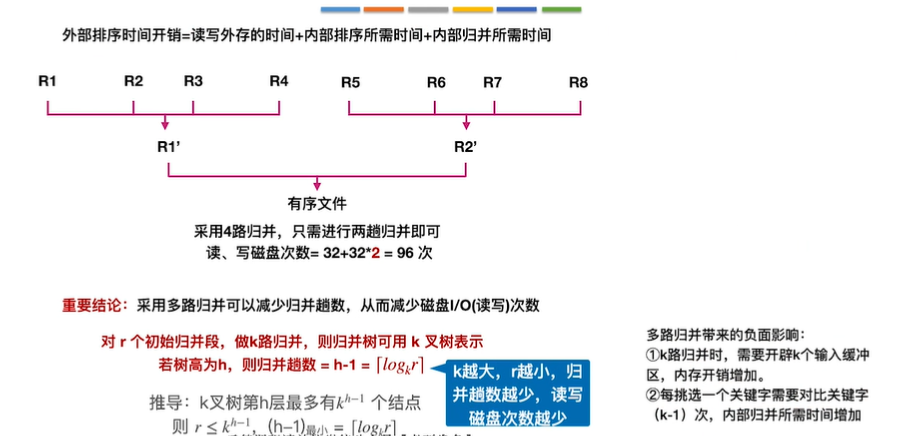
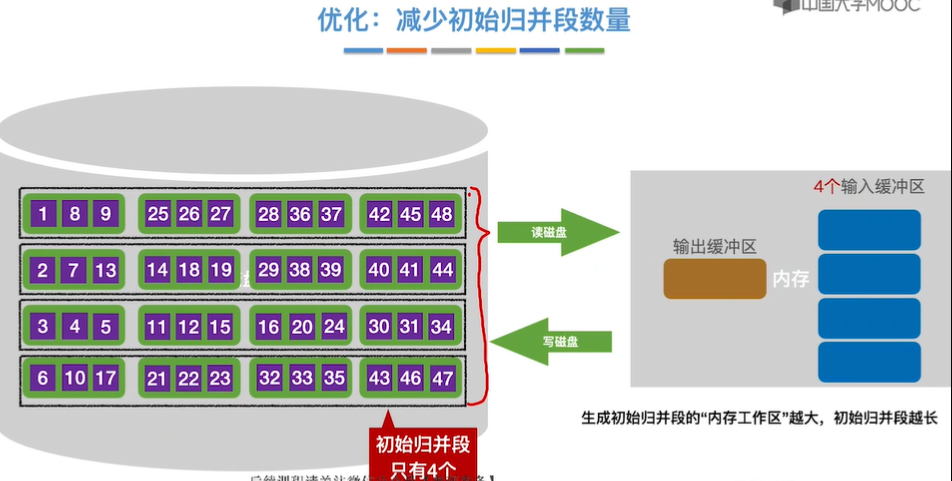
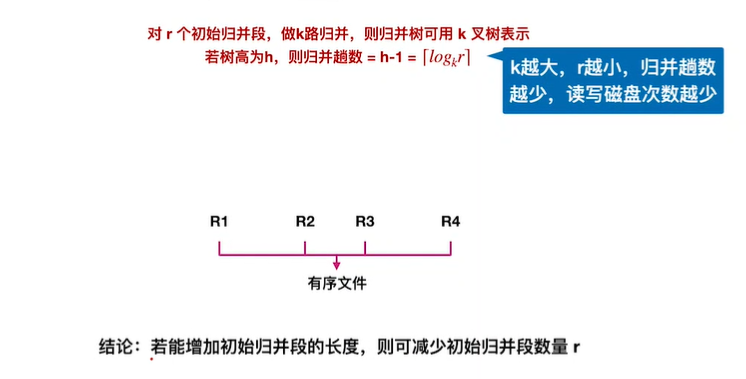

11.败者树
败者树是指可以视为一棵完全二叉树(多了一个头头)。k个叶节点分别是当前参加比较的元素,非叶子结点用来记忆左右子树的”失败者”,而让胜者往上继续进行比较,一直到根节点(考的频率不高,基本是手算的程度)
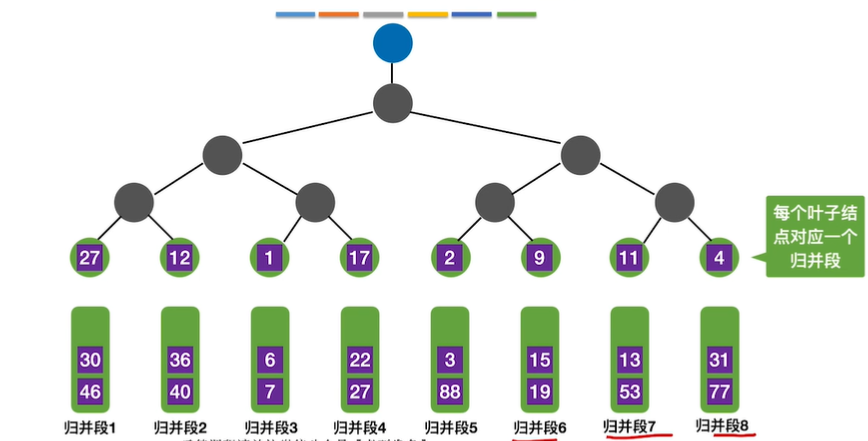
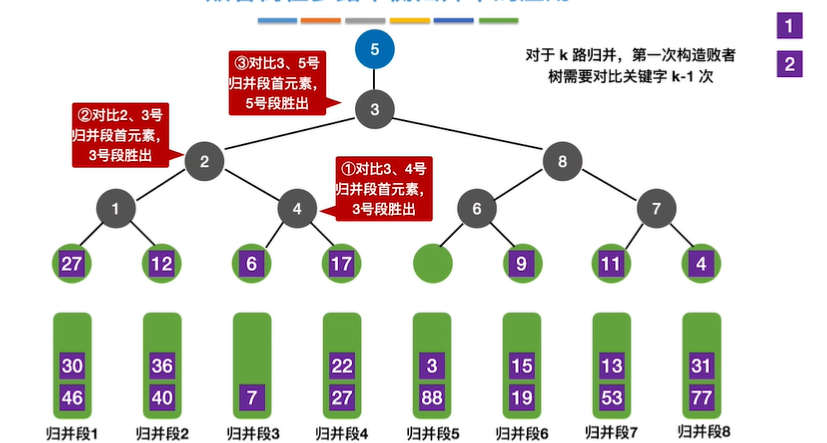
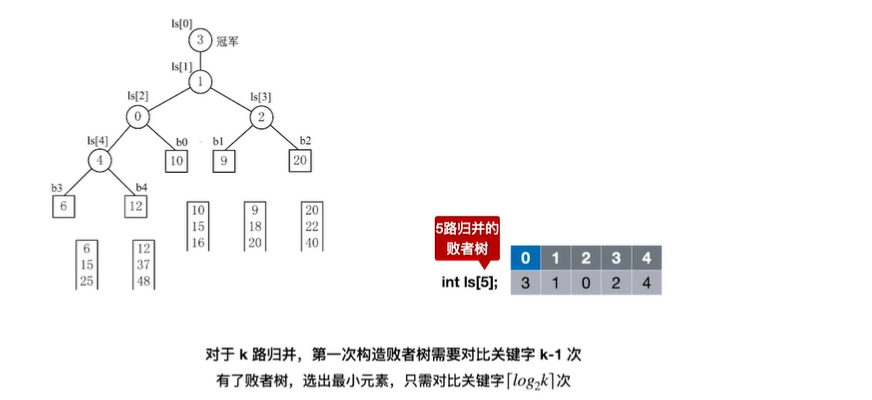
12.置换—选择排序
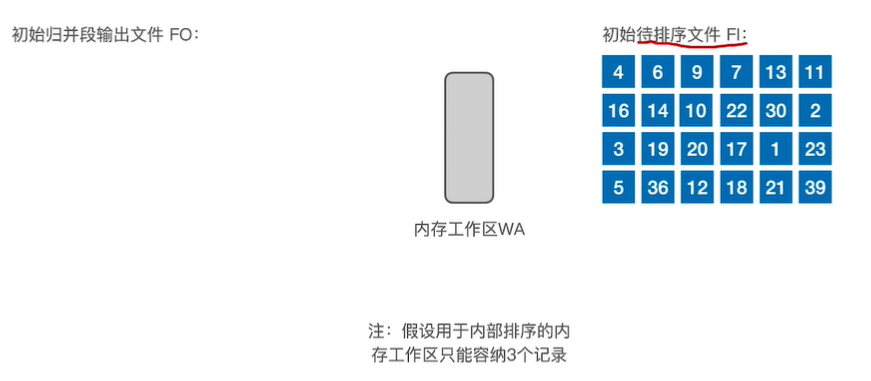
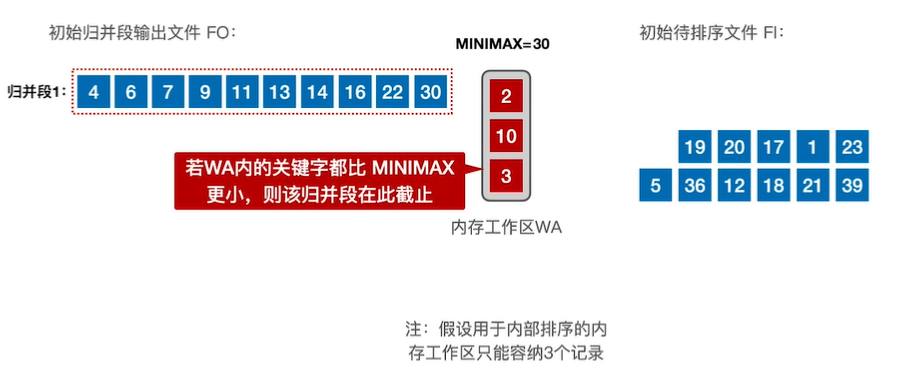


13.最佳归并树

























































